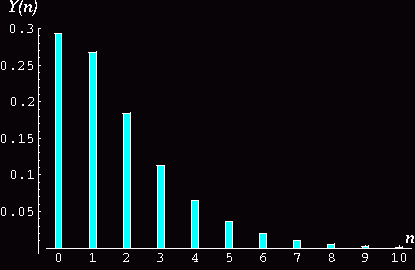APPLICATION DU RECUIT SIMULE A L'INVERSION DE
LA TRANSFORMATION DE POISSON-MANDEL
RESUME
Nous présentons dans ce papier la mise en oeuvre de recuit simulé
ainsi que l'application de deux types de régularisations pour inverser
la transformation de Poisson-Mandel.
INTRODUCTION
La transformation de Poisson-Mandel [1] (TPM) intervient en optique pour
les faibles flux lumineux où l'observation s'effectue en comptage
de photons. La TPM est la transformation qui, appliquée à
la densité de probabilité (DDP) de l'intensité lumineux
à fort flux d'un processus aléatoire donne la répartition
du nombre de photons détectés. Si l'on note X(I) la DDP à
fort flux, la répartition Y(n) du nombre de photons détectés
s'obtient par la relation (1) :
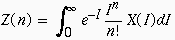 (1)
(1)
qui décrit la TPM. Du point de vue physique, dans de nombreuses
applications, on cherche à obtenir X(I) à partir de la mesure
de Y(n).
Dans le travail que nous présentons, nous avons appliqué
le recuit simulé pour inverser cette équation intégrale.
Nous nous sommes proposés de résoudre numériquement
l'équation (1) pour un cas particulier oò X(I) est constitué
par l'addition de deux structures de speckles non corrélées.
Il s'agit d'un cas classique [2].
La résolution de l'équation (1) est un problème
inverse mal posé car il ne satisfait pas les conditions de l' unicité,
l'existence et la stabilité de la solution vis à vis des
incertitudes de mesures dues au bruit [3]. La résolution numérique
de cette intégrale passe par une étape de discrétisation
qui conduit à :
Y=A.X + b
(2)
oò Y désigne le vecteur des données, A la matrice
de transformationt, X le vecteur des paramètres à estimer
et b le vecteur contenant les bruits de mesures due aux erreurs d'estimation
(bruit statistique). L'équation (1) a une solution (de norme minimale
qui est unique) : X*=A+.Y où A+
désigne l'inverse généralisée, qui est obtenue
comme solution du problème des moindre carrés par minimisation
de :
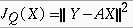 (3)
(3)
oò || .||2 désigne la distance quadratique
.
REGULARISATION
Le mauvais conditionnement de la matrice A ne permet pas d'obtenir une
solution stable du problème. Un principe général pour
s'affranchir des problèmes d'instabilités est celui de la
régularisation. Régulariser un problème c'est admettre
qu'on ne peut pas obtenir la vraie solution à partir des données
entachées d'erreurs, et que le système d'équations
initial ne permet pas de définir un ensemble de solutions possibles
parmis lesquelle une solution acceptable doit être choisie. Ainsi
on est conduit à introduire, dans la formulation du problème,
des informations sur les propriètés "a priori" de la solution.
Cette information se présente sous forme d'une (ou plusieurs) contrainte(s).
En ce qui concerne notre problème une contrainte de douceur est
physiquement raisonnable. On est donc amené à minimiser une
fonctionnelle avec contrainte qui peut s'écrire de façon
générale [4],[5]:
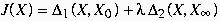 (4)
(4)
oò D1(X,X0) est la distance quadratique
entre X et X0 et D2(X,X) est une distance (à
déterminer) qui a pour rôle de régulariser la solution
X en la contraignant à tendre vers la solution "a priori" (infiniment
lisse) par le biais de l . Le coefficient de régularisation l traduit
l'importance que l'on donne à la contrainte par rapport à
la distance D1(X,X0) qui elle assure le lien entre les données et
le paramètres à estimer. Deux types de régularisations
sont utilisés : A-La première et la plus classique fait partie
de classe des régularisation au sens de Tikhonov [6]. Dans ce cas
l'information "a priori" de douceur est introduite sous forme d'un operateur
différentiel. Ainsi on cherche une solution telle que la norme de
sa dérivée soit inferieure à une limite fixée.
La fonctionnelle à minimiser s'écrit sous la forme suivante
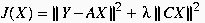 (5)
(5)
où C représente l'opérateur de différentiation.
B-Le principe de régularisation peut Þtre interprété
dans un cadre probabiliste. Dans ce contexte la connaissance "a priori"
de l'objet est traduite par une loi de probabilité. Djafary [3]
montre que le principe de maximum d'entropie permet de déterminer
cette dernière. Si cette connaissance "a priori" se limite à
une contrainte globale sur l'entropie de l'objet, la loi de probabilité
de l'objet s'écrit comme :
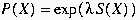 (6)
(6)
avec S(X) donné par la relation ci-dessous :
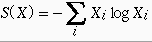 (7)
(7)
La solution X est obtenue en minimisant la fonctionelle ci-dessous :
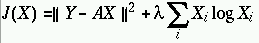 (8)
(8)
RECUIT SIMULE
Le recuit simulé est une méthode de minimisation d'une fonctionnelle
qui a la proprieté de converger vers le minimum glogal. A l'origine
cette technique s'inspire de la physique statistique. En effet, en thermodynamique
statistique à une température T et à l'équilibre
thermique, la probabilité pour qu'une particule se trouve à
un état d'énergie E est donnée par la distribution
de Boltzmann :
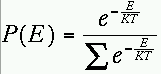 (9)
(9)
Lorsque la température approche zéro, la seule probabilité
non nulle pour que la particule se trouve à un état d'énergie
E correspond à l'état d'énergie minimale du système.
Si on considère un système de particules à haute température,
cet état de la matière correspond à un état
de désordre total (maximum d'entropie). Si on refroidit subitement
celui-ci, le solide que l'on obtiendra ne sera pas dans son état
d'ordre maximal. En effet, en refroidissant brutalement, on fige les particules
dans leurs positions désordonnées et aléatoires (ceci
est un état métastable.). Par contre si on abaisse la température
de façon lente et si pour chaque température on laisse s'établir
l'équilibre thermique, lorsque l'on approche la température
nulle le solide que l'on obtiendra sera dans son état d'énergie
minimale. Donc il se trouvera dans son état d'ordre maximal. Le
recuit simulé est basé sur le mÞme principe, la fonctionnelle
à minimiser joue le rîle de l'énergie.
A une température initiale assez élevée, pour
qu'aucune solution (configuration) ne soit privilégiée, on
part d'une configuration initiale (solution uniforme dans notre cas). On
associe à cette configuration gi une valeur d'énergie
Ei. A cette mÞme température on choisi aléatoirement
un pixel et on lui ajoute (ou retranche) de faÛon aléatoire
une quantité D (le grain). L'énergie associée à
cette configuration est Ei+1. Deux cas peuvent se présenter:
-
La différence des énergies Ei+1-Ei est
négative, cela correspond bien à une décroissance
de l'énergie de l'erreur. On accepte donc cette nouvelle configuration.
-
La différence de l'énergie DE=Ei+1-Ei
est positive ce qui correspond à une augmentation du coût.
L'algorithme de recuit simulé permet d'accepter des configurations
correspondant à une augmentation de coôt si exp(-DE/T) est
plus grand que qu'un nombre aléatoire entre zéro et un (critère
de Metropolis [8]).
On répète cette operation de pérturbation des pixels
de l'image jusqu'à ce que le coôt atteigne une valeur stationnaire,
ce qui correspond à l'équilibre thermique à température
constante. Dès lors que cette convergence est atteinte, on abaisse
d'une petite quantité la température et on recommence le
mÞme procédé. On arrête l'algorithme dès
que le coùt atteint sa convergence asymptotique (système
physique à température nulle). La mise en oeuvre de l'algorithme
va donc consister à contrôler les points suivants :
-
Choix de la température initiale.
-
Choix de la taille de la perturbation.
-
Estimation de l'équilibre approché à une T donnée.
-
Loi de l'abaissement de la température.
-
critère d'arrêt.
1-
La température dans l'algorithme de recuit simulé joue un
rôle très important. C'est elle qui fixe la probabilité
d'accepter ou de refuser les configurations défavorables à
la minimisation (critère de Metropolis [8]). Celui-ci conduit à
accepter des configurations correspondant à une augmentation de
coôt et permet au système de sortir des minima locaux. Le
choix de la température initiale se fait de faÛon empirique
[9]. Il est basé sur principe de taux d'acceptation des configurations:
x=le nombre de configurations augmentant le coôt et acceptées.
e=le nombre de configurations augmentant le coôt. Le rapport de x
sur e définit le taux d'acceptation. Nous avons opté pour
un taux d'acceptation de 80%; ce qui correspond à une température
assez élevée, c'est à dire, exp(-DE/T)>>1.
2-
La taille du grain D est un sujet traité assez évasivement
dans la littérature concernant le recuit simulé. Nous avons
travaillé avec des grains de l'ordre de 1000 ème ou 10000
ème de de l'énergie totale des données expérimentales.
Il est évident qu'un grain très petit augmente considérablement
le temps de calcul, alors que inversement un grain grand conduit à
une solution non optimale [10].
3-
Théoriquement, la convergence du coôt à température
constante est asymptotique. Pour atteindre cette convergence approchée
il faut itérer un grand nombre de fois pour que l'équilibre
s'installe. En pratique ce n'est jamais réalisable, car il faudrait
générer un très grand nombres de configurations pour
atteindre la stationnarité. Nous nous sommes basés sur deux
méthodes différentes:
-
Une méthode empirique est proposée par Kirckpatrick [9].
Elle consiste à fixer un nombre d'itérations pouvant approcher
l'équilibre, tout en gardant un compromis entre le temps de calcul
et la qualité d'image.
-
Nous nous sommes basés sur la convergence de la valeur moyenne relative
du coût [10].
4-
La loi d'abaissement de la température joue un rîle important
dans l'algorithme. Plusieurs méthodes sont proposées dans
la littérature. Nous avons utilisé la loi dite géométrique
:
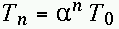 (10)
(10)
Avec 0.85-Le
critère d'arrêt de l'algorithme est basé sur la variation
relative du coût. Soit m1 la valeur moyenne du coût sur N paliers
de températures, m2 étant la moyenne sur N autres paliers
suivants. On considère que la convergence est atteinte quand (m2-m1)/m2
est inférieur à un seuil fixé [10].
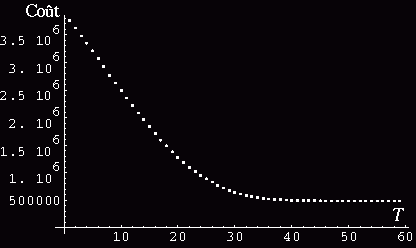
Fig 1: Variation du coût en fonction de la température.
On constate que le coût converge de façon asypmtotique au
delà du 50 ème pas de température.
RESULTATS
Pour le problème qui nous intéresse, la DDP à fort
flux correspondant à la somme de deux structures de speckles X(I)
est donnée par la relation suivante :
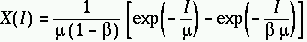 (11)
(11)
L'équation (1) permet de calculer analytiquement la répartition
du nombre de photons Y(n) :
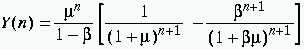 (12)
(12)
où m correspond au nombre moyen de photons par pixel et b désigne
le rapport des intensités des deux structures . Les données
Y(n) sont simulées pour 10000 évènements à
partir de la relation (12).
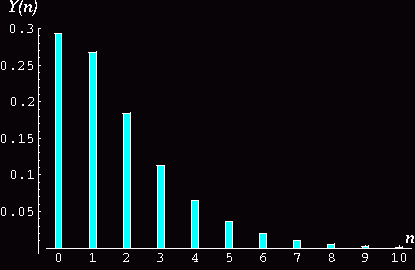
Fig 2-Nous présentons sur la même échelle les données
exactes à partir de la relation (12) ainsi la DDP à fort
flux correspondante (11) déterminée analytiquement suivant
la relation (1).Illustration de la résolution de l'équation
(1) dans le cas théorique (analytique) oò on montre la solution
X(I) en trait plein et la distribution Y(n) sous forme d'histogramme pour
un rapport d'intensité de 0.7 et une moyenne de 1.
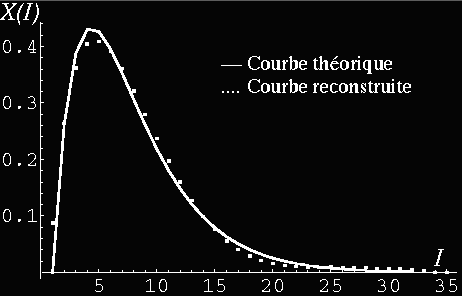
Fig 3 : En pointillé nous présentons la solution reconstruite
X(I) pour m=4 et b=0.7 régularisée par un opérateur
différentiel (gradient l=0.1) pour des données Y(n) simulées
sur 10000 évènements. La solution théorique étant
illustrée en trait plein.
REFERENCES
Aarts A & Korst J Simulated Annealing and Boltzmann Machine. Jones
Wiley & Son (1990).
-
Mandel L Proc.Phys. Soc. 74,233 (1953).
-
Goodman J.W Statistical Optics J.Wiley & Son.
-
Nashed M. Z. Operator Theoriticl and Computational Approaches to Ill Posed
Probeml with Applications to Antenna Theory.IEEE Trans ap 29 p 220-231
(1981).
-
Demoment G. Image Reconstruction and Restoration: Overview of Common Estimation
Structures and Problems. IEEE Trans on Accoustics Speech and Signal proccessing
vol 37 n° 12 dec(1989).
-
Titterington D.M. General Structure of the Regularisation Procedure in
Image Reconstruction. Astronomy and Astrophysics 144,381-387 (1985).
-
Tikhonov A.V & Arsenin V.Y Solutions of Ill Problems. V.H Winston and
Son Washington (1977).
-
Mohammed-Djafary A.A. Synthèse de Fourier Multivariables à
Maximum d'Entropie.Thèse de Doctorat D'Etat. Univ Paris-sud Orsay
(1987).
-
Metropolis
-
Kirckpatrick .S & Gelatto.C.O Optimisation by Simulated annealing.
Sciences, Vol 220, n°4598 13 May (1983).
-
:Sultani.F Inversion de la Transformation de Poisson par Recuit simulé.
Rapport de DEA. Université de Nice.
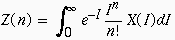 (1)
(1)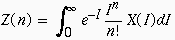 (1)
(1)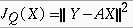 (3)
(3)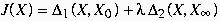 (4)
(4)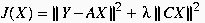 (5)
(5)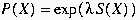 (6)
(6)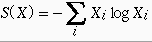 (7)
(7)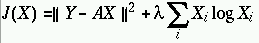 (8)
(8)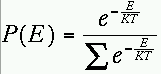 (9)
(9)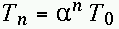 (10)
(10)
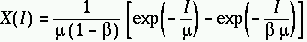 (11)
(11)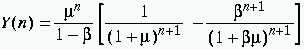 (12)
(12)