Coefficient de transmission
d'un prisme
On considère une onde plane sinusoidale se propageant dans le
vide avec un vecteur d'onde 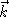 et une pulsation
et une pulsation  . Une telle onde s'écrit, en notation complexe :
. Une telle onde s'écrit, en notation complexe : 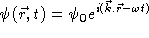 . Cette onde se propage dans une direction faisant un angle
. Cette onde se propage dans une direction faisant un angle  avec le plan (yz) et un angle
avec le plan (yz) et un angle 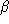 avec le plan (xz) (faites un dessin).
avec le plan (xz) (faites un dessin).
-
Pour
 et
et 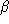 petits, et en restant dans la limite du premier ordre, écrire les
3 composantes du vecteur d'onde
petits, et en restant dans la limite du premier ordre, écrire les
3 composantes du vecteur d'onde 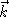 en fonction de
en fonction de  ,
, 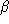 et la longueur d'onde
et la longueur d'onde 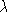 . (on rappelle que
. (on rappelle que 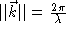 , ça va ètre utile pour trouver
, ça va ètre utile pour trouver 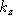 ). Réécrire alors l'expression de l'onde dans cette approximation.
). Réécrire alors l'expression de l'onde dans cette approximation.
-
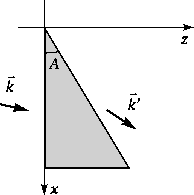
Soit un prisme d'angle au sommet A petit et d'indice n
éclairé par une onde plane se propageant dans le plan (xz)
avec un angle d'incidence
 par rapport à la normale à la face d'entrée du prisme.
par rapport à la normale à la face d'entrée du prisme.
-
En appliquant les lois de Descartes, trouver les composantes du vecteur
d'onde
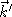 à la sortie du prisme. On se placera dans l'approximation des petits
angles (
à la sortie du prisme. On se placera dans l'approximation des petits
angles (  petit) (on dit aussi approximation de Gauss ou optique paraxiale).
petit) (on dit aussi approximation de Gauss ou optique paraxiale).
-
Ecrire en fonction de
 et de A les expressions des ondes incidente et transmise, dans un
plan
et de A les expressions des ondes incidente et transmise, dans un
plan 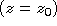 après la sortie du prisme. Montrer alors que l'interposition du
prisme sur le trajet de l'onde incidente revient à multiplier celle-ci
par un coefficient de transmission que l'on déterminera.
après la sortie du prisme. Montrer alors que l'interposition du
prisme sur le trajet de l'onde incidente revient à multiplier celle-ci
par un coefficient de transmission que l'on déterminera.
Ce résultat, vrai dans l'approximation de Gauss et établi
pour le prisme, s'applique à tout objet transparent d'épaisseur
e(x,y) : il est assimilable à un écran plat de coefficient
de transmission 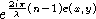 .
.
![]() et une pulsation
et une pulsation ![]() . Une telle onde s'écrit, en notation complexe :
. Une telle onde s'écrit, en notation complexe : ![]() . Cette onde se propage dans une direction faisant un angle
. Cette onde se propage dans une direction faisant un angle ![]() avec le plan (yz) et un angle
avec le plan (yz) et un angle ![]() avec le plan (xz) (faites un dessin).
avec le plan (xz) (faites un dessin).

![]() .
.