La lentille


 

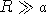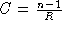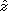On considère une lentille plan convexe de diamètre 2a en verre d'indice n. La face avant de cette lentille est plane tandis que la face arrière est une portion de sphère de rayon de courbure tex2html_wrap_inline129 . On appelle convergence le nombre tex2html_wrap_inline131 . Cette lentille est éclairée par une onde plane arrivant dans la direction tex2html_wrap_inline133 .

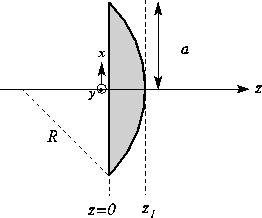
tex2html_wrap191

  1. Ecrire en fonction de a et de R l'épaisseur de verre e(x,y) que traverse un rayon incident (on prendra l'origine des x,y au centre de la face arrière de la lentille).

  2.  Ecrire dans l'approximation de Gauss l'amplitude de l'onde en tex2html_wrap_inline143 . Comparer à l'amplitude qu'aurait l'onde plane incidente en tex2html_wrap_inline143 si la lentille était absente. Montrer que l'interposition de la lentille sur le trajet de l'onde plane incidente se traduit sur les amplitudes par un terme multiplicatif t(x,y) que l'on explicitera (on dit que la lentille est un filtre de phase). Montrer que lorsque l'on place plusieurs lentilles accolées les unes aux autres, les convergences s'ajoutent.

  3.  Ecrire dans l'approximation de Gauss l'équation de la surface d'onde à la sortie (lieu des points où l'amplitude complexe de l'onde est constante, c'est une équation du type z=f(x,y)). Pourquoi dit-on que cette onde est sphérique ? Que se passe-t-il au point z=1/C ? Quelle est la focale de cette lentille ?

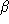  4.  Cas général : on éclaire maintenant cette lentille par une onde plane inclinée de deux angles tex2html_wrap_inline77 et tex2html_wrap_inline81 . Donner l'amplitude de l'onde à la sortie et l'équation de la surface d'onde. Montrer que cette onde converge en un point que l'on déterminera et qui se trouve dans le plan z=1/C.

  5.  On place maintenant un point source sur l'axe optique de la lentille en 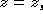tex2html_wrap_inline159 . Ce point-source émet une onde sphérique qui s'écrit

    6.  

     

    displaymath161

    dans l'approximation de Gauss, (avec 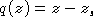tex2html_wrap_inline163 ). Montrer que l'onde à la sortie est sphérique aussi et trouver la position de l'image du point-source.

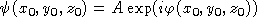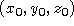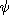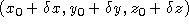  6.  Soit tex2html_wrap_inline165 l'amplitude complexe d'une onde quelconque en un point de coordonnées tex2html_wrap_inline167 . En effectuant un développement de la phase au premier ordre, donner une expression approchée de tex2html_wrap_inline169 en un point très voisin de coordonnées tex2html_wrap_inline171 . Remarquer que cette expression correspond à celle d'une onde plane dont on précisera le vecteur d'onde. 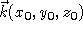On peut ainsi montrer que toute onde peut localement être approximée à une onde plane avec un vecteur d'onde tex2html_wrap_inline173 qui dépend de la position.

  7.  En se plaçant dans le cas de la question 4, montrer que l'onde à la sortie de la lentille est associée à une série de rayons qui convergent en un point que l'on déterminera (et qui ne devrait pas être très différent de celui de la question 3).

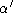  8.  On se place dans le plan (y=0) et on considère une onde qui arrive avec une inclinaison tex2html_wrap_inline77 par rapport à l'axe optique. On caractérise un rayon lumineux par deux paramètres : son inclinaison tex2html_wrap_inline77 et la coordonnée x du point où il arrive sur la lentille. Si tex2html_wrap_inline183 et x' désignent le rayon à la sortie de la lentille, établir la matrice qui lie tex2html_wrap_inline187 à tex2html_wrap_inline189 (matrice de transfert de la lentille).