Les caustiques

Cet exercice est inspiré du partiel de Décembre 1994

1. On considère une lentille mince située dans le plan z=0. Cette lentille est éclairée par une onde plane arrivant sous incidence normale. On suppose que la lentille est à symétrie de révolution et on travaille dans le plan (xz).
   
   
1. Ecrire, en fonction de la distance focale f de la lentille, l'amplitude complexe de l'onde à la sortie de la lentille dans le plan z=0.
   
   
2.  En déduire l'équation x(z) (z;SPMgt;0) d'un rayon issu de la lentille en x=x0 et passant par le point M(x,z). Combien de rayons passent par le point M ?
   
   
3.  Montrer que tous les rayons se croisent en un point et calculer les coordonnées de ce point (point focal ou foyer de la lentille).
   
   
2. On considère cette fois une lentille qui présente un défaut de forme se traduisant par des termes d'ordre supérieur dans la phase de l'onde à la sortie. On travaille toujours dans le plan (xz) et on suppose que la phase s'écrit en z=0 :
   
   






1. Etablir l'équation des rayons dans la région z>0.
2.  Montrer qu'en un point M(x,z) après la sortie, il peut passer deux rayons différents, issus de 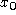 et de  .
3.  A quelle condition ne passe-t'il aucun rayon par le point M ? A quelle condition n'y passe-t'il qu'un seul rayon ? Donner alors l'équation de la caustique et montrer que les rayons sont tangents à la caustique.
   
   
4.  Montrer que la courbe caustique est du second degré autour du point z=f.
   
   
5.  Quel est l'angle que font entre eux deux rayons passant par un point (x<0,z=f) ? Expliquer qualitativement l'observation d'interférences dans cette région et calculer l'interfrange.