Cavité laser

 

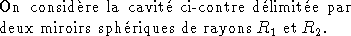
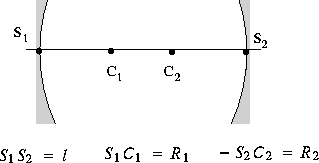
1. Montrer qu'un miroir de rayon R est équivalent à une lentille de convergence 2/R.
2.  Montrer alors que la cavité est équivalente à un système de 2 lentilles de focales 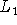 et 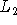 , répété à l'infini comme ci-dessous.

 

 



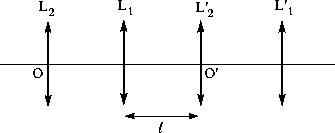
3. Ecrire la matrice P de passage de O à O' (correspondant à un aller-retour dans la cavité). On rappelle que le déterminant de P doit être égal à 1.
   
   
4.  A quelle conditions sur les coefficients de P, un rayon 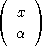 reste-t-il confiné dans la cavité après un nombre infini de réflexions ? (condition de stabilité). Ecrire cette condition de stabilité en fonction de 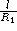 et 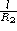 . Dessiner les régions de stabilité dans un diagramme (  ,  ).
   
   
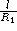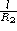5.  On considère un point-source placé dans un plan z=q avant le point O. A quelle distance q' du point O' se trouve son image ? A quelles conditions sur les coefficients de P a-t-on q'=q ? Ce cas correspond-il à une cavité stable ou instable ? Commentaires ?
   
   
6.  On rappelle qu'une onde sphérique s'écrit, dans l'approximation de Gauss,

 

 





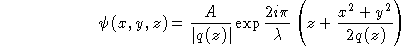
On s'intéresse à une onde reproduite identique à elle-même après un aller-retour dans la cavité. Discuter la nature d'une telle onde dans le cas d'une cavité stable et d'une cavité instable.



7.  Dans le cas où q(z) est complexe, on écrit 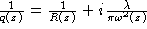 . Réécrire l'expression de  . Que représentent R(z) et  ? Dans le cas d'une cavité formée de deux miroirs identiques ( 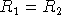 ), que valent R et  au niveau des miroirs ?
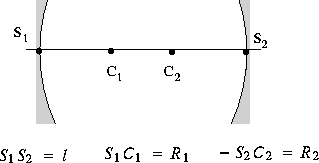
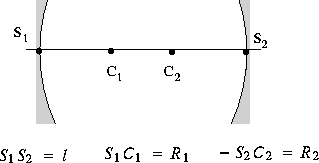