Pouvoir de résolution

Un cas particulier important est celui pour lequel $P(x_1,y_1)$ est une fonction porte circulaire de diamètre $D$ . Ce cas de figure est très fréquent dans la mesure où les lentilles (ou objectifs d'appareil photo ou miroirs de télescope) sont généralement taillés avec une section circulaire. Dans ce cas la réponse impulsionnelle est la fonction d'Airy

$$R(\alpha,\beta)=\frac{\pi^2 D^4}{4} J_{1c}\left(\frac{\pi D \sqrt{\alpha^2+\beta^2}}\lambda\right)^2$$

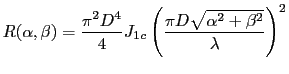
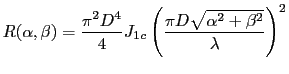
Le graphe de cette fonction est représentée figure ci-dessous. Le lobe central de l'image est entouré d'un anneau noir de rayon angulaire $1.22\lambda/D$ (les variables $\alpha$ et $\beta$ sont des angles).

Image d'un point-source par une pupille ciculaire de diamètre $D$ (réponse impulsionnelle $R(\alpha ,\beta )$ ) : c'est la fonction d'Airy. A gauche la coupe pour $\beta =0$ , au milieu une représentation en perspective cavalière et à droite l'aspect visuel de l'image (une tache entourée d'anneaux).

Si l'on considère un objet constituée de deux points-source séparés d'un angle $\theta$ , l'image produite est la somme de deux fonctions d'Airy déparées du même angle : $I(\alpha,\beta)=R(\alpha,\beta)+R(\alpha-\theta,\beta)$ . le pouvoir séparateur est défini comme la plus petite valeur de $\theta$ pour laquelle les deux taches d'Airy sont discernables. Selon le critère de Rayleigh, ces images sont justes séparées si le maximum de l'une coïncide avec le premier zéro de l'autre, soit pour

$$\theta=1.22\frac{\lambda}{D}$$

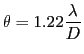
La figure ci-après illustre ce critère de Rayleigh. C'est lui qui impose le pouvoir de résolution des télescopes en astronomie : un diamètre de 1 m offre ainsi une résolution de 0.1 seconde d'arc (angle correspondant à une pièce de monnaie vue à 4 km), tandis qu'il faudrait un diamètre de 100 m pour voir un homme sur la Lune (angle de 1 milliseconde d'arc).

Image de deux points-source par une pupille ciculaire de diamètre $D$ . La limite de résolution est atteinte lorsque l'angle de séparation entre les deux points-source est égal à $1.22\frac {\lambda }{D}$ , c'est le critère de Rayleigh (figures de la colonne du milieu).