La relation objet image est une convolution dans l'espace direct. Dans l'espace de Fourier (variables 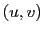 ) elle devient un produit
) elle devient un produit
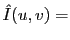
Cte
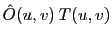
avec 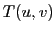 la fonction de transfert qui illustre un filtrage linéaire des fréquences spatiales présentes dans l'objet
la fonction de transfert qui illustre un filtrage linéaire des fréquences spatiales présentes dans l'objet 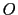 .
. 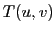 est la transformée de Fourier de la réponse impulsionnelle
est la transformée de Fourier de la réponse impulsionnelle
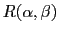 . Il vient, après application du théorème de Wiener-Kinchin :
. Il vient, après application du théorème de Wiener-Kinchin :
avec 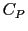 l'autocorrélation de la fonction pupille définie par
l'autocorrélation de la fonction pupille définie par
Il est courant de normaliser la fonction de transfert, c'est à dire de la diviser par sa valeur à l'origine 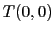
Dans le cas d'une pupille circulaire de diamètre 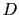 , la fonction
, la fonction
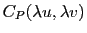 est l'intégrale de recouvrement de deux disques séparés d'une distance
est l'intégrale de recouvrement de deux disques séparés d'une distance
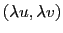 . Le calcul donne (en divisant par la valeur à l'origine)
. Le calcul donne (en divisant par la valeur à l'origine)
avec
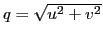 . C'est une fonction centrosymétrique appelée parfois ``chapeau chinois''. Son graphe est représenté figure ci-dessous. Cette fonction possède une fréquence de coupure
. C'est une fonction centrosymétrique appelée parfois ``chapeau chinois''. Son graphe est représenté figure ci-dessous. Cette fonction possède une fréquence de coupure
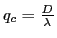 au delà de laquelle elle est nulle. Toute fréquence angulaire supérieure à
au delà de laquelle elle est nulle. Toute fréquence angulaire supérieure à 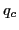 ne sera pas transmise entre l'objet et l'image (ce qui, dans l'espace direct se traduit par le fait que tout détail plus petit que l'angle
ne sera pas transmise entre l'objet et l'image (ce qui, dans l'espace direct se traduit par le fait que tout détail plus petit que l'angle
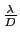 ne sera pas visible dans l'image).
ne sera pas visible dans l'image).
Fonction de transfert d'une pupille circulaire de diamètre 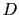 (fonction dite ``chapeau chinois''). Elle est centrosymétrique et possède une fréquence de coupure
(fonction dite ``chapeau chinois''). Elle est centrosymétrique et possède une fréquence de coupure
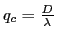 .
.
|
|
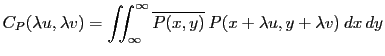
![$\displaystyle T(u,v)=\frac{2}{\pi}\left[
\arccos\left(\frac{\lambda q}D\right) - \frac{\lambda q}D\sqrt{1-\left(\frac{\lambda q}D\right)^2}
\right]
$](img199.gif)