
Soit
![]() les coordonnées d'un point
les coordonnées d'un point ![]() sur la source
sur la source ![]() , et
, et ![]() un élément de surface autour de
un élément de surface autour de ![]() . On note
. On note
![]() l'amplitude complexe émise par l'élément de surface
l'amplitude complexe émise par l'élément de surface ![]() et
et
![]() l'intensité moyenne correspondante (avec
l'intensité moyenne correspondante (avec
![]() ). La fonction
). La fonction
![]() a la dimension d'une intensité par unité de surface de la source. Elle est appelée distribution spatiale de brillance de la source
a la dimension d'une intensité par unité de surface de la source. Elle est appelée distribution spatiale de brillance de la source ![]() .
.
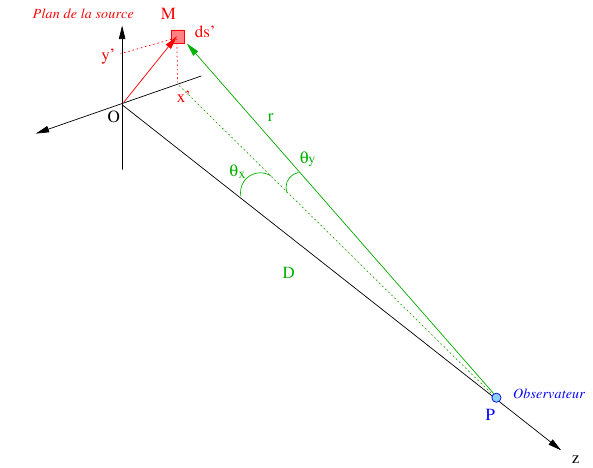
On appelle ![]() le point sur lequel se trouve l'observateur et
le point sur lequel se trouve l'observateur et ![]() la distance
la distance ![]() . Soit
. Soit ![]() le vecteur
le vecteur ![]() joignant l'observateur à un point de la source. On a
joignant l'observateur à un point de la source. On a
![]() . Les quantités
. Les quantités
![]() et
et
![]() représentent la direction dans laquelle est vu le point
représentent la direction dans laquelle est vu le point ![]() depuis
depuis ![]() (tangentes des angles
(tangentes des angles ![]() et
et ![]() indiqués sur la figure). La quantité
indiqués sur la figure). La quantité
![]() est l'angle solide sous lequel est vu l'élément de surface
est l'angle solide sous lequel est vu l'élément de surface ![]() depuis l'observateur.
depuis l'observateur.
L'élément de surface ![]() autour du point
autour du point ![]() émet une intensité
émet une intensité
On écrira
La quantité
![$\textstyle \parbox{12cm}{
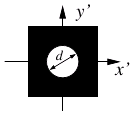
\item[{Disque uniforme :}] Un disque uniforme de diam...
...ne constante) et �met dans tout l'espace une intensit� totale $K\; \pi d^2/4$.}$](img52.gif)

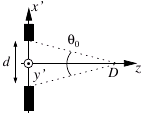
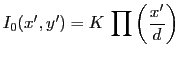
en utilisant les mêmes notations que pour le disque. Sa distribution angulaire de brillance s'écrit
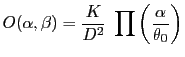
avec
Sa distribution angulaire de brillance s'écrit