Franges d'Young avec une source large
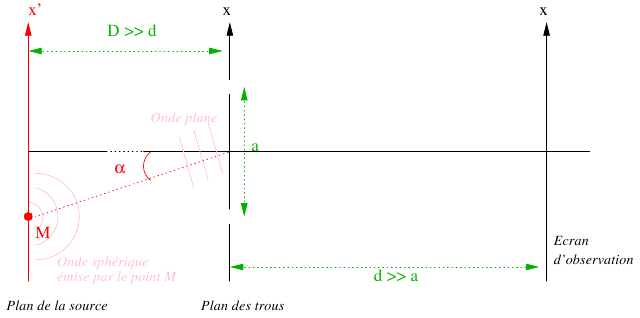
Ce paragraphe est un cas particulier simple du problème des interférences avec de la lumière provenant de sources larges. Considérons le dispositif suivant :
Une source large est placée dans un plan
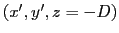 . Elle éclaire un interféromètre à trous d'Young placé dans le plan
. Elle éclaire un interféromètre à trous d'Young placé dans le plan 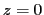 . La source est supposée monochromatique (longueur d'onde
. La source est supposée monochromatique (longueur d'onde 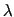 ). Les trous distants de
). Les trous distants de 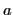 sont alignés suivant
sont alignés suivant 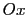 . On observe les franges sur un écran placé à une distance
. On observe les franges sur un écran placé à une distance 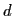 du plan des trous.
du plan des trous.
On prendra les conventions suivantes :
- On suppose
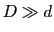 et
et 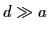 de telle sorte que les conditions de la diffraction de Fraunhofer soient réalisées.
de telle sorte que les conditions de la diffraction de Fraunhofer soient réalisées.
- On notera
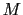 un point de la source (coordonnées
un point de la source (coordonnées 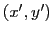 dans le plan de la source).
dans le plan de la source).
- On notera
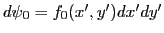 l'amplitude de l'onde sphérique émise par le point
l'amplitude de l'onde sphérique émise par le point 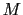 . Cette onde sphérique est plane en arrivant dans le plan des trous (approximation de Fraunhofer).
. Cette onde sphérique est plane en arrivant dans le plan des trous (approximation de Fraunhofer).
- On noreta
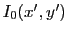 et
et
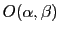 les distributions spatiale de angulaire brillance. On supposera dans un premier temps que ces fonctions sont symétriques (paires).
les distributions spatiale de angulaire brillance. On supposera dans un premier temps que ces fonctions sont symétriques (paires).
- On supposera que la source est peu étendue (support borné) et on se placera dans les conditions de l'optique paraxiale (
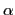 et
et 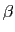 s'identifient aux angles
s'identifient aux angles 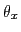 et
et 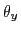 ).
).
La technique de calcul de l'intensité des franges d'interférences consiste à prendre la source point par point, de calculer les franges d'Young produites par chaque point de la source, et d'intégrer sur la source. Considérons donc un point 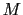 de la source. Ce point rayonne dans le demi-espace
de la source. Ce point rayonne dans le demi-espace 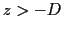 une onde sphérique d'amplitude complexe (la dépendance temporelle en
une onde sphérique d'amplitude complexe (la dépendance temporelle en
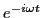 est omise dans cette présentation (elle disparaitra de toutes façons dans le calcul de l'intensité)
est omise dans cette présentation (elle disparaitra de toutes façons dans le calcul de l'intensité)
cette onde est plane en arrivant dans le plan 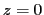 . Elle arrive sous l'incidence oblique caractérisée par les deux cosinus directeurs
. Elle arrive sous l'incidence oblique caractérisée par les deux cosinus directeurs 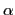 et
et 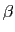 (ici assimilables aux angles). Ainsi l'amplitude complexe dans le plan
(ici assimilables aux angles). Ainsi l'amplitude complexe dans le plan 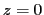 s'écrit
s'écrit
Le coefficient de transmission 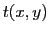 du masque est modélisé par la somme de deux distributions
du masque est modélisé par la somme de deux distributions 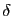 :
:
et l'amplitude complexe à la sortie du masque est
Dans le plan d'observation 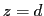 , puisque
, puisque 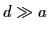 on fait l'approximation de Fraunhofer et l'on écrit l'amplitude compexe en
on fait l'approximation de Fraunhofer et l'on écrit l'amplitude compexe en 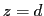 comme la transformée de Fourier de celle en
comme la transformée de Fourier de celle en 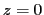 :
:
ce qui s'écrit comme
L'intensité produite dans le plan d'observation par l'élément de surface 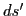 est alors égale à
est alors égale à
Soit, en fonction des directions 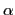 et
et 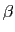
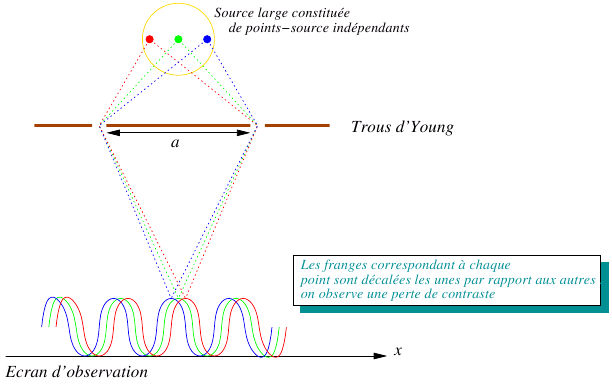
On trouve des franges d'Young dont l'origine est située en
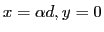 . Ces franges sont produites par l'élément de surface
. Ces franges sont produites par l'élément de surface 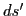 qui se trouve dans la direction
qui se trouve dans la direction 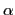 au dessus de l'axe
au dessus de l'axe 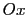 . Lorsque l'on va considérer l'ensemble de la source, on sera amené à intégrer des franges d'Young décalées les une par rapport aux autres comme le schématise la figure ci-après :
. Lorsque l'on va considérer l'ensemble de la source, on sera amené à intégrer des franges d'Young décalées les une par rapport aux autres comme le schématise la figure ci-après :
L'intensité résultant de l'intégrale sur la source s'écrit, en utilisant l'identité
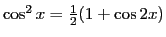 :
:
une formule qui parait compliquée mais qui peut s'écrire très simplement à l'aide de la transformée de Fourier de la fonction
 si l'on utilise les identités
si l'on utilise les identités
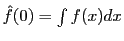 et
et
 e
e![$ \;[e^{ix}]$](img97.gif) . Ainsi
. Ainsi
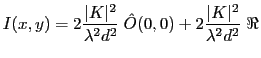
e
![$\displaystyle \;\left[\hat O\left(\frac{a}{\lambda},0\right) \; \exp 2 i\pi \frac{ax}{\lambda d} \right]
$](img99.gif)
On écrit 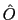 sous forme trigonométrique :
sous forme trigonométrique :
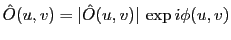 . Il vient
. Il vient
soit encore
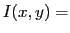
Cte
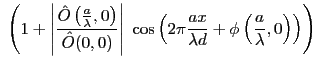
Cette intensité correspond à un système de franges de même période
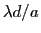 que dans le cas d'une source ponctuelle. Il y a deux différences :
que dans le cas d'une source ponctuelle. Il y a deux différences :
- Un changement d'origine dûe à la phase de
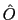 . Le systême de franges est centré en
. Le systême de franges est centré en
qui disparait si la source est symétrique (diaphragme circulaire centré sur l'axe optique par exemple).
- et surtout la présence d'un terme de contraste
qui est indépendant de la position 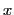 dans le champ d'interférences, mais dépend de l'écart entre les trous.
dans le champ d'interférences, mais dépend de l'écart entre les trous.
Si l'on choisit une source symétrique (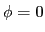 ), on observe deux phénomènes quand on fait varier l'écart entre les trous
), on observe deux phénomènes quand on fait varier l'écart entre les trous 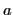 en l'augmentant à partir de
en l'augmentant à partir de 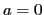 :
:
- les franges se resserrent (interfrange proportionnel à
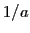
- le contraste, égal à 1 pour
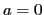 , change avec
, change avec 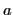 (en général il diminue pour des sources classiques)
(en général il diminue pour des sources classiques)
La figure ci-dessous illustre et résume ces observations dans le cas où la source observée a une distribution angulaire de brillance
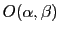 gaussienne ; la T.F. d'une gaussienne étant une gaussienne, la fonction de visibilité des franges (leur contraste) va décroitre de manière Gaussienne avec
gaussienne ; la T.F. d'une gaussienne étant une gaussienne, la fonction de visibilité des franges (leur contraste) va décroitre de manière Gaussienne avec 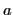 .
.
Illustration de la perte de contraste des franges lors d'une expérience de trous d'Young éclairés par une source large. Sur la colonne de gauche la fonction contraste 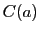 en fonction de la distance
en fonction de la distance 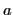 entre les trous. Au milieu l'aspect visuel des franges. A droite le graphe de l'intensité des franges. Les graphes correspondent à 6 écarts différents
entre les trous. Au milieu l'aspect visuel des franges. A droite le graphe de l'intensité des franges. Les graphes correspondent à 6 écarts différents 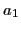 ,
, 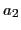 ...des trous.
...des trous.
![\includegraphics[width=\textwidth]{eps/cspat_contr_gauss.eps}](img112.png) |

![]() de la source. Ce point rayonne dans le demi-espace
de la source. Ce point rayonne dans le demi-espace ![]() une onde sphérique d'amplitude complexe (la dépendance temporelle en
une onde sphérique d'amplitude complexe (la dépendance temporelle en
![]() est omise dans cette présentation (elle disparaitra de toutes façons dans le calcul de l'intensité)
est omise dans cette présentation (elle disparaitra de toutes façons dans le calcul de l'intensité)
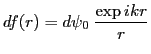
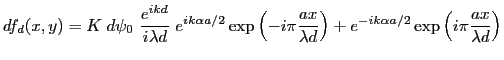
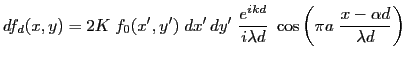
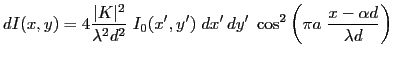
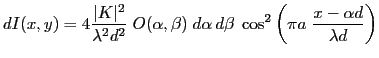
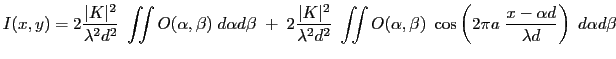
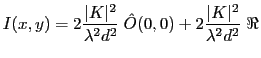 e
e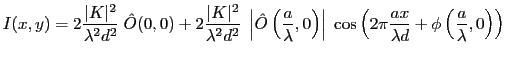
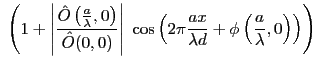
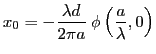
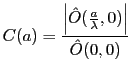
![\includegraphics[width=\textwidth]{eps/cspat_contr_gauss.eps}](img112.png)