
Dans l'expérience de trous d'Young du paragraphe précédent, le contraste des franges est proportionnel à la fonction
![]() . Il fait intervenir la transformée de Fourier
. Il fait intervenir la transformée de Fourier
![]() de la distribution de brillance. Or les propriétés générale de la transformation de Fourier imposent que si une fonction
de la distribution de brillance. Or les propriétés générale de la transformation de Fourier imposent que si une fonction ![]() a une largeur
a une largeur ![]() dans le plan direct, sa T.F.
dans le plan direct, sa T.F. ![]() a une largeur
a une largeur
![]() dans le plan de Fourier. Cette propriété se généralise à deux variables : une fonction
dans le plan de Fourier. Cette propriété se généralise à deux variables : une fonction ![]() de largeur
de largeur ![]() dans la direction
dans la direction ![]() et
et ![]() dans la direction
dans la direction ![]() a une T.F.
a une T.F.
![]() dont la largeur vaut
dont la largeur vaut
![]() dans la direction
dans la direction ![]() et
et
![]() dans la direction
dans la direction ![]() . Ainsi, si on appelle
. Ainsi, si on appelle
![]() la largeur (diamètre angulaire) de la source
la largeur (diamètre angulaire) de la source
![]() dans la direction
dans la direction ![]() , la fonction
, la fonction
![]() est de de largeur proportionnelle à
est de de largeur proportionnelle à
![]() et la fonction contraste
et la fonction contraste ![]() est de largeur proportionnelle à
est de largeur proportionnelle à
![]() : le contraste tend vers 0 lorsque
: le contraste tend vers 0 lorsque
![]() . On définira la largeur de cohérence spatiale par
. On définira la largeur de cohérence spatiale par
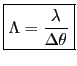 |
(1.2) |
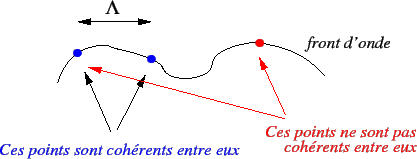
Physiquement, ![]() représente la distance maximale entre deux points du front d'onde pour lesquels les vibrations sont cohérentes. Et si l'on réalise une expérience de trous d'Young, on ne verra plus de franges quand la distance entre les trous devient
représente la distance maximale entre deux points du front d'onde pour lesquels les vibrations sont cohérentes. Et si l'on réalise une expérience de trous d'Young, on ne verra plus de franges quand la distance entre les trous devient ![]() .
.
| Etoile Betelgeuse |
|
|
| Le Soleil |
|
|
| Ampoule vue à 1 m |
|
|