![\includegraphics[width=12cm]{eps/ctemp_src_pct_mir.eps}](img172.png)
|
![\includegraphics[width=12cm]{eps/ctemp_src_pct_mir.eps}](img172.png)
|
Comme précédemment, on commence par écrire l'intensité des franges dans le cas monochromatique. La source ![]() aurait dans ce cas une amplitude complexe qui s'écrirait, dans l'approximation paraxiale :
aurait dans ce cas une amplitude complexe qui s'écrirait, dans l'approximation paraxiale :
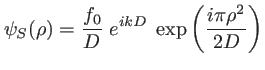
Avec
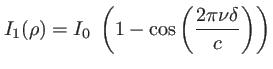
avec
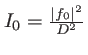 et
et
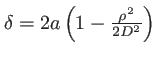 la différence de marche. Le signe - devant le cosinus est dû au déphasage de
la différence de marche. Le signe - devant le cosinus est dû au déphasage de
Dans le cas polychromatique, on remplace ![]() par
par
![]() (intensité dans la bande de fréquences
(intensité dans la bande de fréquences
![]() ). Le calcul de l'intensité
). Le calcul de l'intensité ![]() en
en ![]() ne pose pas de problème (ondes sphériques dans l'approximation paraxiale). Il vient
ne pose pas de problème (ondes sphériques dans l'approximation paraxiale). Il vient
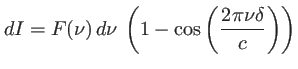
En introduisant le retard
L'intégrale sur la fréquence permet finalement d'écrire l'intensité :
![$\displaystyle I(\tau)=\hat P(0)\:\left[1 -\frac{\vert\hat P(\tau)\vert}{\hat P(0)} \cos(2 \pi \nu_0\tau-\phi(\tau))\right]
$](img186.png)
qui fait à nouveau apparaitre le terme de contraste
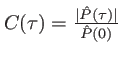 . Prenons l'exemple du spectre du paragraphe précédent :
. Prenons l'exemple du spectre du paragraphe précédent :
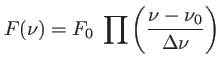
avec
![$\displaystyle I(\rho)=F_0 \Delta\nu \; \left(1-\mbox{sinc}\left[2\pi a\frac{\De...
...ht] \; \cos \frac{4\pi a}{\lambda}\left[ 1-\frac{\rho^2}{2 D^2}\right] \right)
$](img188.png)
Cette fonction ne dépend que de
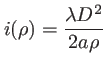
inversement proportionnel à
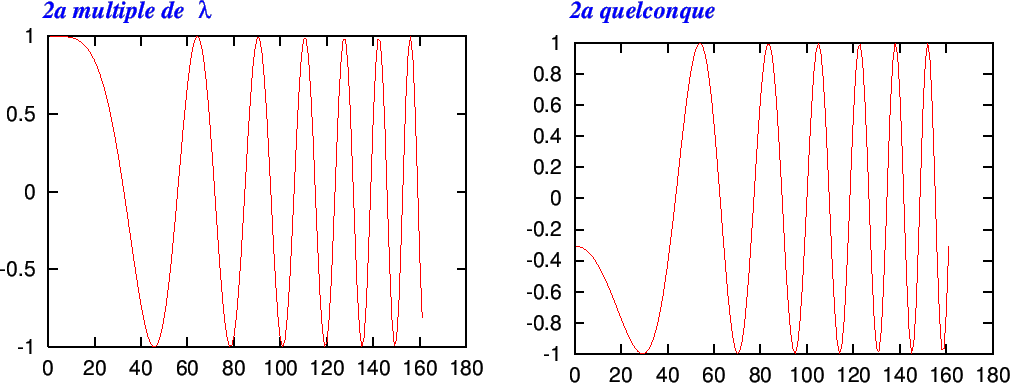
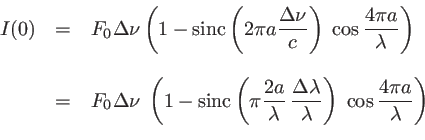
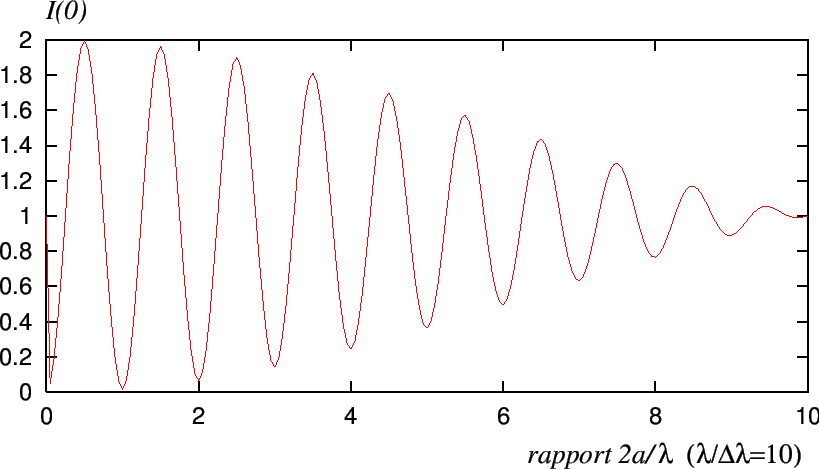
et présente un ``maximum'' lorsque le rapport
![]() (ordre d'interférence au centre) est un multiple demi-entier de la logueur d'onde. Demi-entier à cause du déphasage de
(ordre d'interférence au centre) est un multiple demi-entier de la logueur d'onde. Demi-entier à cause du déphasage de ![]() à la réflexion sur le miroir. A mesure que
à la réflexion sur le miroir. A mesure que ![]() augmente, l'intensité à l'origine diminue (influence du sinus cardinal) et devient très faible lorsque la différence de marche
augmente, l'intensité à l'origine diminue (influence du sinus cardinal) et devient très faible lorsque la différence de marche ![]() dépasse la longueur de cohérence
dépasse la longueur de cohérence
![]() .
.
L'allure des franges d'interférence est la suivante (en noir et blanc sur la figure, mais en réalité l'oeil verra des couleurs comme pour les trous d'Young)
