Degré de cohérence : application aux franges d'Young
On considère une onde plane quasi-monochromatique de spectre
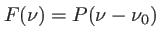 arrivant sous incidence normale sur un écran percé de deux trous quasi-ponctuels. La direction de propagation est notée
arrivant sous incidence normale sur un écran percé de deux trous quasi-ponctuels. La direction de propagation est notée 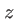 , le plan des trous est pris comme origine des
, le plan des trous est pris comme origine des 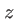 . La distance entre les trous est
. La distance entre les trous est 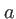 , la distance entre le plan des trous et le plan d'observation est
, la distance entre le plan des trous et le plan d'observation est 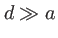 (on suppose valable l'approximation de la diffraction à l'infini entre les plans
(on suppose valable l'approximation de la diffraction à l'infini entre les plans 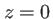 et
et 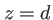 ). On cherche à calculer l'intensité en un point
). On cherche à calculer l'intensité en un point  de coordonnées
de coordonnées 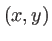 dans le plan
dans le plan 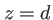 . Le schéma est le suivant :
. Le schéma est le suivant :

- L'amplitude en
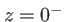 vaut
vaut 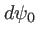 .
.
- En
 après le passage à travers les trous l'amplitude s'écrit (en omettant la constante multiplicative représentant la surface des trous)
après le passage à travers les trous l'amplitude s'écrit (en omettant la constante multiplicative représentant la surface des trous)
.
- En
 l'amplitude est la TF de
l'amplitude est la TF de 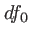 (diffraction à l'infini). Il vient
(diffraction à l'infini). Il vient
- L'intensité correspondante est, en fonction de
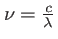 :
:
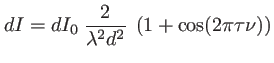 |
(3.1) |
Avec
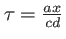 , cette variable possède la dimension d'un temps. Il s'agit du temps de retard entre les deux ondes interférant en
, cette variable possède la dimension d'un temps. Il s'agit du temps de retard entre les deux ondes interférant en 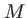 (différence de marche parcourue à la vitesse de la lumière). L'intensité
(différence de marche parcourue à la vitesse de la lumière). L'intensité 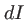 est celle d'une figure de franges d'Young de constraste 1 et d'interfrange
est celle d'une figure de franges d'Young de constraste 1 et d'interfrange
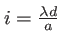 . C'est la situation habituelle dans le cas monochromatique.
. C'est la situation habituelle dans le cas monochromatique.
Fig. 3.3:
Franges d'Young pour trois longueurs d'onde
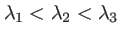 . L'interfrange, proportionnel à la longueur d'onde, est différent pour les trois sytèmes de franges. En éclairage polychromatique, les 3 systèmes de franges s'ajoutent (en intensité) et donnent une figure complexe présentant une frange brillante au milieu (différence de marche nulle). Les graphes du bas représentent l'aspect visuel des franges dans ce cas (couleurs) et le graphe de l'intensité totale (en trait plein).
. L'interfrange, proportionnel à la longueur d'onde, est différent pour les trois sytèmes de franges. En éclairage polychromatique, les 3 systèmes de franges s'ajoutent (en intensité) et donnent une figure complexe présentant une frange brillante au milieu (différence de marche nulle). Les graphes du bas représentent l'aspect visuel des franges dans ce cas (couleurs) et le graphe de l'intensité totale (en trait plein).
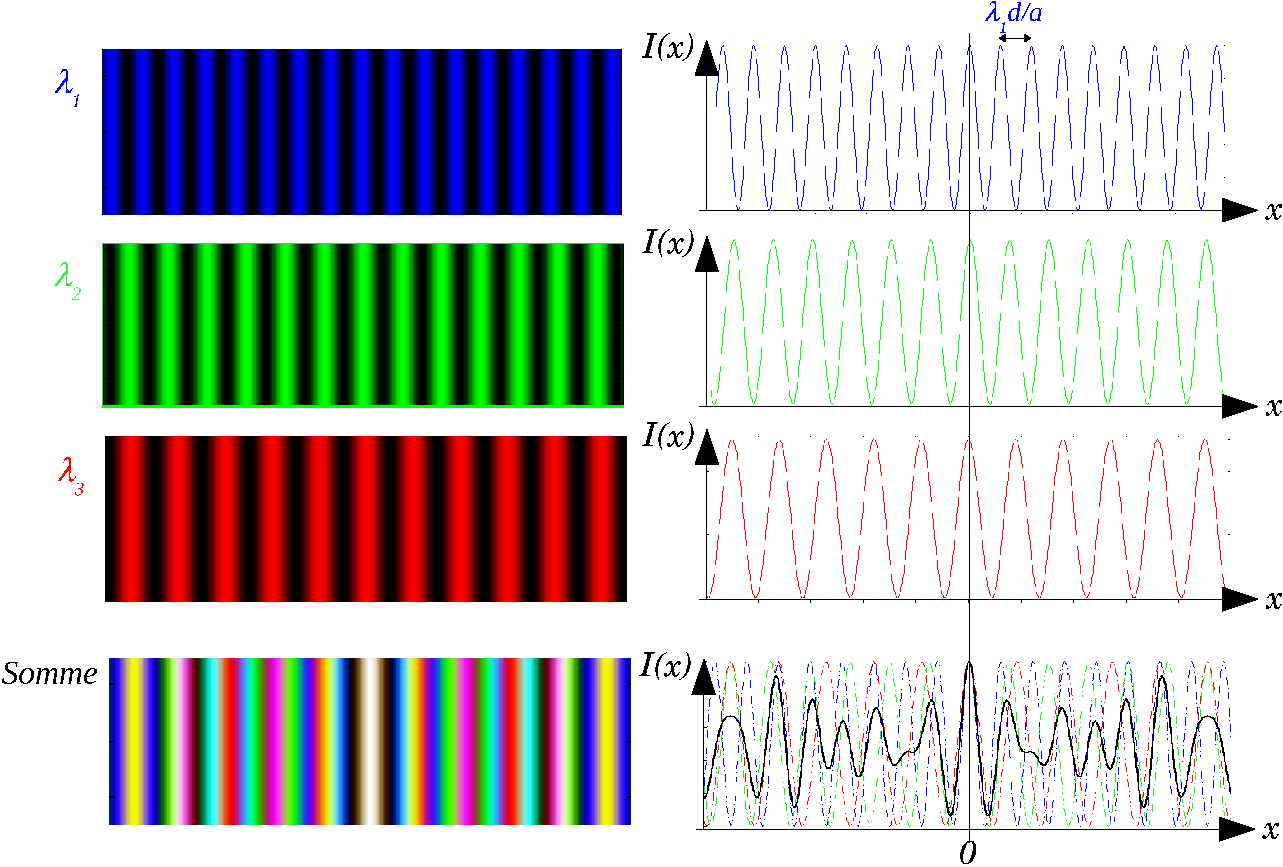 |
Chaque fréquence (ou chaque longueur d'onde) produit un système de franges d'Young avec un interfrange dépendant de la longueur d'onde comme illustré par la figure 3.3. Puisque des ondes de fréquences différentes dont incohérentes entre elles, ces franges d'Young s'ajoutent en intensité. La frange centrale (correspondant à 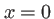 ) est brillante quelle que soit
) est brillante quelle que soit 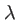 , on aura donc toujours une frange brillante au centre.
, on aura donc toujours une frange brillante au centre.
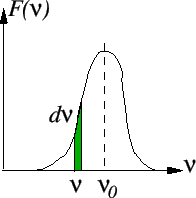
Le calcul de l'intensité se fait en intégrant 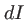 sur la fréquence. Il vient :
sur la fréquence. Il vient :
Le spectre de la lumière, 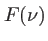 est une fonction réelle, on peut écrire
est une fonction réelle, on peut écrire
Il apparait la transformée de Fourier
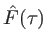 du spectre. En introduisant la fonction profil par la relation
du spectre. En introduisant la fonction profil par la relation
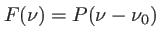 , et en utilisant la propriété
, et en utilisant la propriété
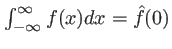 il vient
il vient
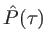 est la TF du profil de raie, quantité a priori complexe sauf si
est la TF du profil de raie, quantité a priori complexe sauf si 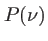 est symétrique (cas des Lorentziennes ou des gaussiennes). Nous poserons
est symétrique (cas des Lorentziennes ou des gaussiennes). Nous poserons
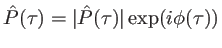 . L'intensité s'écrit alors, toujours en fonction de la variable
. L'intensité s'écrit alors, toujours en fonction de la variable 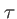 :
:
On peut dégager trois termes :
Voici l'aspect du champ d'interférences tel qu'il serait observé
par l'oeil :

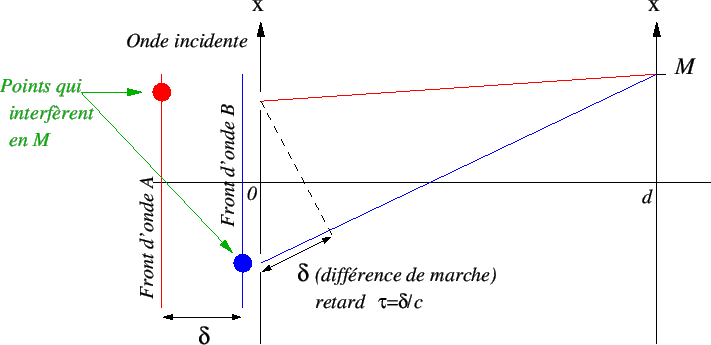
Fig. 3.4:
Ce schéma illustre comment deux portions de l'onde incidente situées sur deux fronts d'ondes 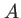 et
et 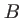 interfèrent en
interfèrent en 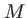 . Le front d'onde
. Le front d'onde 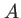 est en retard d'une quantité
est en retard d'une quantité 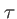 sur
sur 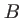 avant le plan des trous. Ce retard est rattrapé ensuite à cause de la différence de marche. Faire une expérience de trous d'Young revient à faire interférer deux fronts d'onde de l'onde incidente, décalés temporellement de
avant le plan des trous. Ce retard est rattrapé ensuite à cause de la différence de marche. Faire une expérience de trous d'Young revient à faire interférer deux fronts d'onde de l'onde incidente, décalés temporellement de 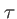 . Le décalage temporel est ajustable car il est proportionnel à
. Le décalage temporel est ajustable car il est proportionnel à 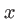 . Plus
. Plus 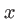 est grand, plus le retard est important.
est grand, plus le retard est important.
|
|
L'expérience des trous d'Young réalise l'interférence de deux ondes planes décalées temporellement de 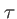 . Ces 2 ondes planes ayant été prélevées par les trous sur l'onde incidente, tout se passe comme si l'on faisait interférer deux fronts d'ondes incidents décalés temporellement de
. Ces 2 ondes planes ayant été prélevées par les trous sur l'onde incidente, tout se passe comme si l'on faisait interférer deux fronts d'ondes incidents décalés temporellement de 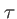 , comme schématisé sur la figure 3.4.
On appelle degré complexe de cohérence la quantité
, comme schématisé sur la figure 3.4.
On appelle degré complexe de cohérence la quantité
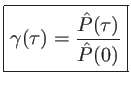 |
(3.2) |
C'est un nombre complexe dont le module est compris entre 0 et 1 (c'est le contraste des franges). Si
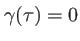 il n'y a pas d'interférences. Les ondes qui interfèrent en
il n'y a pas d'interférences. Les ondes qui interfèrent en 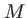 sont incohérentes entre elles.
sont incohérentes entre elles.
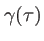 mesure la cohérence mutuelle de deux fronts d'onde séparés temporellement de
mesure la cohérence mutuelle de deux fronts d'onde séparés temporellement de 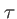 .
.
Le profil de raie s'écrit dans ce cas
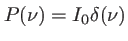 . L'intensité, en fonction de
. L'intensité, en fonction de 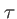 , est
, est
soit, en fonction de 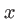 (changement de variable
(changement de variable
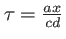 )
)
et l'on retrouve l'expression bien connue des franges de contraste 1 et d'interfrange
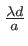
Le profil de raie s'écrit
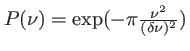 ,
, 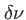 est la largeur de la raie. Sa TF s'écrit
est la largeur de la raie. Sa TF s'écrit
Elle est réelle, la fonction contraste 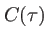 également. L'intensité s'écrit, en fonction de
également. L'intensité s'écrit, en fonction de 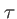 :
:
et en fonction de 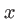 :
:
avec
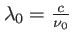 la longueur d'onde centrale de la vibration. Le graphe de l'intensité est représenté en figure 3.5. Les franges sont présentes à l'intérieur d'une enveloppe définie par les courbes
la longueur d'onde centrale de la vibration. Le graphe de l'intensité est représenté en figure 3.5. Les franges sont présentes à l'intérieur d'une enveloppe définie par les courbes
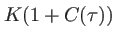 et
et
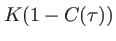 (avec
(avec
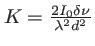 ). Cette enveloppe a une largeur inversement propotionnelle à
). Cette enveloppe a une largeur inversement propotionnelle à 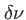 . Au delà de la zône centrale, le contraste des franges diminue rapidement et l'on observe une teinte uniforme.
. Au delà de la zône centrale, le contraste des franges diminue rapidement et l'on observe une teinte uniforme.
Fig. 3.5:
Franges d'Young dans le cas où l'éclairage se fait avec un profil de raie gaussien (largeur
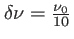 ). En haut, graphe de l'intensité exprimé en fonction de la position
). En haut, graphe de l'intensité exprimé en fonction de la position 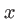 dans le champ d'interférences, ou du retard
dans le champ d'interférences, ou du retard 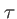 entre les deux ondes (
entre les deux ondes (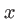 et
et 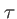 étant proportionnels, le graphe est le même). Au mileu : aspect visuel des interférences (représenté en noir et blanc). En bas : le cas monochromatique (
étant proportionnels, le graphe est le même). Au mileu : aspect visuel des interférences (représenté en noir et blanc). En bas : le cas monochromatique (
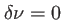 ) pour comparaison.
) pour comparaison.
|
|
On considère cette fois la superposition de deux vibrations de fréquences très proches
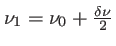 et
et
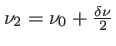 (avec
(avec
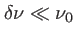 ). On fait l'hypothèse que les intensités associées à ces ondes sont identiques (le profil est alors symétrique autour de la fréquence centrale
). On fait l'hypothèse que les intensités associées à ces ondes sont identiques (le profil est alors symétrique autour de la fréquence centrale 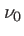 ). Le profil de raie s'écrit
). Le profil de raie s'écrit
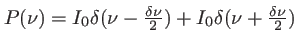 .
.
La TF du profil s'écrit
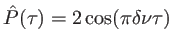 . C'est à nouveau une fonction réelle et paire. L'intensité des franges s'écrit alors (en fonction de
. C'est à nouveau une fonction réelle et paire. L'intensité des franges s'écrit alors (en fonction de  ) :
) :
Le graphe de l'intensité est représenté en figure 3.6. Cette fois les franges ne disparaissent pas lorsque
 comme dans le cas précédent. Mais on a un terme d'enveloppe
comme dans le cas précédent. Mais on a un terme d'enveloppe
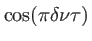 qui définit des ``paquets'' de franges. Ces paquets sont de largeur proportionnelle
qui définit des ``paquets'' de franges. Ces paquets sont de largeur proportionnelle
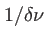 , ils dépendent de la différence des fréquences des deux ondes (ce phénomène est analogue aux battements que l'on peut entendre entre deux ondes sonores de fréquences voisines). Entre deux paquets successifs, le contraste s'annule (disparition des franges), puis s'inverse (signe - du terme
, ils dépendent de la différence des fréquences des deux ondes (ce phénomène est analogue aux battements que l'on peut entendre entre deux ondes sonores de fréquences voisines). Entre deux paquets successifs, le contraste s'annule (disparition des franges), puis s'inverse (signe - du terme
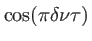 ). Ce phénomène d'inversion de contraste est caractérisé par une inversion des franges brillantes et des franges sombres.
). Ce phénomène d'inversion de contraste est caractérisé par une inversion des franges brillantes et des franges sombres.
Fig. 3.6:
Franges d'Young dans le cas où l'éclairage se fait avec une raie double (
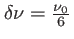 ). En haut, graphe de l'intensité exprimé en fonction du retard
). En haut, graphe de l'intensité exprimé en fonction du retard 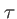 entre les deux ondes. Au mileu : aspect visuel des interférences. En bas : le cas monochromatique (
entre les deux ondes. Au mileu : aspect visuel des interférences. En bas : le cas monochromatique (
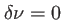 ) pour comparaison. Entre deux paquets de franges le contraste s'inverse (les franges brillantes deviennent sombres et vice-versa)
) pour comparaison. Entre deux paquets de franges le contraste s'inverse (les franges brillantes deviennent sombres et vice-versa)
|
|
![\includegraphics[width=10cm]{eps/ctemp_young.eps}](img62.png)
![\includegraphics[width=10cm]{eps/ctemp_young.eps}](img62.png)


![$\displaystyle df_0(x,y)=d\psi_0\:\left[\delta\left(x-\frac a 2,y \right) +\delta\left(x+\frac a 2,y \right)\right]$](img67.png)
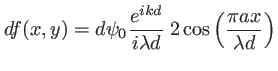

![]() ) est brillante quelle que soit
) est brillante quelle que soit ![]() , on aura donc toujours une frange brillante au centre.
, on aura donc toujours une frange brillante au centre.
![]() sur la fréquence. Il vient :
sur la fréquence. Il vient :
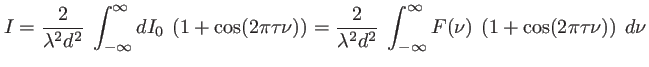
![$\displaystyle I=\frac{2}{\lambda^2 d^2}\: \left[\int_{-\infty}^\infty F(\nu)\:d...
...left\{\int_{-\infty}^\infty F(\nu) e^{-2i \pi \tau \nu}\: d\nu\right\}
\right]
$](img78.png)
![$\displaystyle I=\frac{2}{\lambda^2 d^2}\:\left[\hat P(0) +{\Re}\mbox{e}\;\left\{\hat P(\tau) e^{-2 i \pi \tau \nu_0}\right\}\right]
$](img81.png)
![$\displaystyle I=\frac{2 \hat P(0)}{\lambda^2 d^2}\:\left[1 +\frac{\vert\hat P(\tau)\vert}{\hat P(0)} \cos(2 \pi \nu_0\tau-\phi(\tau))\right]
$](img84.png)
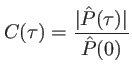

![]() . Ces 2 ondes planes ayant été prélevées par les trous sur l'onde incidente, tout se passe comme si l'on faisait interférer deux fronts d'ondes incidents décalés temporellement de
. Ces 2 ondes planes ayant été prélevées par les trous sur l'onde incidente, tout se passe comme si l'on faisait interférer deux fronts d'ondes incidents décalés temporellement de ![]() , comme schématisé sur la figure 3.4.
On appelle degré complexe de cohérence la quantité
, comme schématisé sur la figure 3.4.
On appelle degré complexe de cohérence la quantité 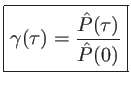
![$\displaystyle I=\frac{2 I_0}{\lambda^2 d^2}\:\left[1 + \cos(2 \pi \nu_0\tau)\right]
$](img93.png)
![$\displaystyle I(x)=\frac{2 I_0}{\lambda^2 d^2}\:\left[1 + \cos\left(2\pi \frac{ax}{\lambda d}\right)\right]
$](img94.png)
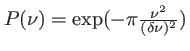 ,
, ![$\displaystyle I=\frac{2 I_0\delta\nu}{\lambda^2 d^2}\:\left[1 + \exp(-\pi \tau^2 \delta\nu^2)\: \cos(2 \pi \nu_0\tau)\right]
$](img100.png)
![$\displaystyle I(x)=\frac{2 I_0\delta\nu}{\lambda^2 d^2}\:\left[1 + \exp\left(-\...
...lta\nu}{cd}\right)^2\right)\cos\left(2\pi \frac{ax}{\lambda_0 d}\right)\right]
$](img101.png)
![\includegraphics[width=14cm]{eps/ctemp_frange_raiegauss.eps}](img106.png)
![]() . C'est à nouveau une fonction réelle et paire. L'intensité des franges s'écrit alors (en fonction de
. C'est à nouveau une fonction réelle et paire. L'intensité des franges s'écrit alors (en fonction de ![]() ) :
) :
![$\displaystyle I=\frac{2 I_0}{\lambda^2 d^2}\:\left[1 + \cos(\pi \delta\nu \tau)\: \cos(2 \pi \nu_0\tau)\right]
$](img112.png)
![\includegraphics[width=14cm]{eps/ctemp_frange_raiedbl.eps}](img116.png)