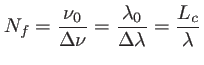On s'intéresse à une onde quasi-monochromatique dont le profil 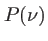 a une largeur
a une largeur 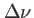 autour de la fréquence centrale (
autour de la fréquence centrale (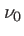 ). Le contraste
). Le contraste 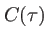 des franges est proportionnel au module
des franges est proportionnel au module
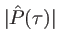 de la transformée de Fourier du profil de raie : il possède alors une largeur
de la transformée de Fourier du profil de raie : il possède alors une largeur
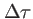 qui, d'après le principe d'incertitude, doit vérifier
qui, d'après le principe d'incertitude, doit vérifier
Dans le cas d'une onde quasi-monochromatique, le contraste est donc une fonction lentement variable devant la période des franges (figure 3.7).
Fig. 3.7:
Allure du graphe de l'intensité en fonction du retard 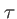 dans le cas d'un spectre quasi-monochromatique de largeur
dans le cas d'un spectre quasi-monochromatique de largeur 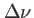 . Deux valeurs sont importantes : l'interfrange
. Deux valeurs sont importantes : l'interfrange 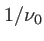 et la taille de l'enveloppe
et la taille de l'enveloppe
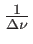 .
.
|
|
On appelle temps de cohérence la quantité
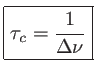 |
(3.3) |
C'est une mesure de la largeur de la fonction contraste 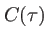 . Si le retard
. Si le retard 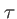 entre les deux fronts d'onde est grand devant
entre les deux fronts d'onde est grand devant 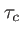 alors
alors
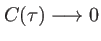 et les franges disparaissent. Les deux fronts d'onde ne produisent plus d'interférence : ils sont devenus mutuellement incohérents. C'est le cas de l'exemple de la figure 3.5. L'onde perd sa capacité à interférer avec elle-même retardée d'un temps supérieur au temps de cohérence.
et les franges disparaissent. Les deux fronts d'onde ne produisent plus d'interférence : ils sont devenus mutuellement incohérents. C'est le cas de l'exemple de la figure 3.5. L'onde perd sa capacité à interférer avec elle-même retardée d'un temps supérieur au temps de cohérence.
On appelle longueur de cohérence la quantité
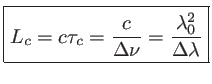 |
(3.4) |
C'est la distance que parcourt l'onde à la vitesse de lumière pendant le temps 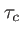 . C'est une mesure de la distance maximun entre deux fronts d'onde cohérents, comme illustré sur la figure
. C'est une mesure de la distance maximun entre deux fronts d'onde cohérents, comme illustré sur la figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png)
Fig. 3.8:
La longueur de cohérence d'une onde est la distance maximale entre deux fronts d'onde cohérents, c'est à dire capable d'interférer entre eux. Elle est infinie pour une onde parfaitement monochromatique.
|
|
La longueur de cohérence est un paramètre commode pour évaluer par exemple la différence de marche maximale entre les deux bras d'un interféromètre de Michelson : cette différence de marche ne devra pas excéder la longueur de cohérence.
Le nombre 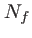 de franges visibles est le rapport entre la largeur de la fonction contraste et la période des franges :
de franges visibles est le rapport entre la largeur de la fonction contraste et la période des franges :
Quelques ordres de grandeur :
| Source |
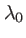 (nm)
(nm) |
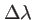 (nm)
(nm) |
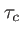 (s)
(s) |
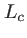 (m)
(m) |
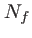
|
| Laser He-Ne |
632.8 |
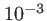
|
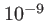
|
0.3 |
50 000 |
| Raie rouge de l'hydrogène |
656.2 |
0.1 |
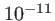
|
0.004 |
6500 |
| Lumière du Soleil |
500 |
400 |
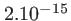
|
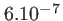
|
1 |
| Lumière blanche + filtre étroit |
500 |
20 |
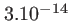
|
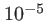
|
25 |
On peut remarquer que toutes ces quantités sont des propriétés intrinsèques de l'onde et ne dépendent pas de l'interféromètre utilisé. Remarquons aussi qu'il est impossible d'obtenir des interférences avec la lumière blanche du Soleil (1 frange visible seulement), mais que la traversée d'un filtre permet d'augmenter le temps de cohérence en réduisant la largeur de bande.
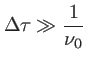
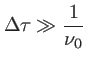
![\includegraphics[width=11cm]{eps/ctemp_franges.eps}](img120.png)
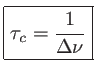
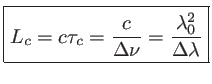
![\includegraphics[width=11cm]{eps/ctemp_long_coh.eps}](img125.png)