Licence de Physique -- Devoir d'optique
Coronographie, Nulling et toute cette sorte de
choses
Pour le 23 Mai 2003 -- Travail en petits groupes
de 2 à 4 personnes
Une des préoccupations des astronomes de ce début du
XXIe siècle est la détection et l'étude des planètes
extra-solaires. Une centaine ont été observées à
ce jour par des méthodes indirectes depuis la détection de
la toute première, 51 Peg, par l'équipe de Michel Mayor en
1995. L'enjeu est maintenant la détection directe de ces exoplanètes
par imagerie optique. L'obstacle principal à surmonter est l'extrème
différence d'éclat entre l'étoile et sa planète-compagnon.
Dans le visible, le rapport d'intensité est d'un milliard ; il
est un peu plus favorable dans l'infrarouge (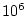 ) mais encore hors
de portée des techniques actuelles... ou en tout cas d'il y a quelques
années puisqu'un nouveau champ de recherches dans l'imagerie à
très haute dynamique est apparu il y a peu. L'idée centrale
de ces techniques est d'éteindre la lumière provenant de l'étoile
pour faire ressortir celle de la planète. Les solutions techniques
s'orientent vers deux voies : le nulling, ou extinction par
interférence destructice, et la coronographie basée sur une
occulation par des masques adaptés. L'objectif de ce problème
est de faire une étude de principe de l'un de ces instruments, le
``Coronographe Interférentiel Achromatique'', développé
à l'observatoire de la Côte d'Azur par l'équipe de Jean
Gay.
) mais encore hors
de portée des techniques actuelles... ou en tout cas d'il y a quelques
années puisqu'un nouveau champ de recherches dans l'imagerie à
très haute dynamique est apparu il y a peu. L'idée centrale
de ces techniques est d'éteindre la lumière provenant de l'étoile
pour faire ressortir celle de la planète. Les solutions techniques
s'orientent vers deux voies : le nulling, ou extinction par
interférence destructice, et la coronographie basée sur une
occulation par des masques adaptés. L'objectif de ce problème
est de faire une étude de principe de l'un de ces instruments, le
``Coronographe Interférentiel Achromatique'', développé
à l'observatoire de la Côte d'Azur par l'équipe de Jean
Gay.
On considère l'interféromètre de Michelson de la figure
ci-dessous. La lumière incidente est séparée en deux
moitiés égales par la lame séparatrice (Sp). Une partie
de la lumière (onde 1) est réfléchie par le miroir plan
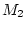 et atteint le plan d'observation (E). L'autre partie de la
lumière (onde 2) se réfléchit sur le miroir
et atteint le plan d'observation (E). L'autre partie de la
lumière (onde 2) se réfléchit sur le miroir 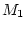 . On appelle
. On appelle 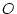 le point milieu de la séparatrice,
le point milieu de la séparatrice,
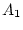 et
et 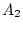 les points milieux des miroirs
les points milieux des miroirs 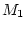 et
et 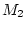 , et
, et 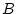 le point d'origine des
coordonnées sur l'écran
le point d'origine des
coordonnées sur l'écran 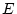 . On pose
. On pose 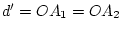 ,
, 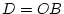 .
.
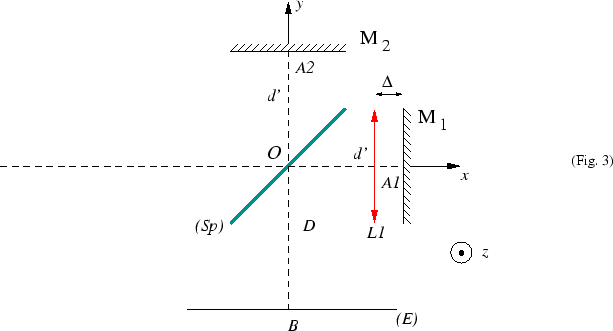
On intercale entre 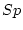 et
et 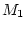 une lentille convergente
une lentille convergente
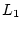 de focale
de focale 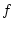 . Cette lentille est placée
à une distance
. Cette lentille est placée
à une distance 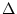 de
de 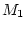 . On éclaire
l'ensemble par une onde plane monochromatique de longueur d'onde
. On éclaire
l'ensemble par une onde plane monochromatique de longueur d'onde 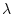 provenant de la gauche de la figure et se propageant dans
le sens des
provenant de la gauche de la figure et se propageant dans
le sens des 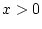 . On se place dans les conditions de l'otique
paraxiale et on négligera les effets de diffraction par les bords
des mitoirs et de la lentille (ce qui revient à considérer
ceux-ci comme infinis).
. On se place dans les conditions de l'otique
paraxiale et on négligera les effets de diffraction par les bords
des mitoirs et de la lentille (ce qui revient à considérer
ceux-ci comme infinis).
- Montrer que l'onde 2, après son double passage par la lentille,
est sphérique et calculer la position de son centre
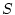 . Quelle doit ètre la valeur de
. Quelle doit ètre la valeur de 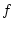 pour que
pour que
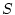 soit situé entre
soit situé entre 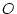 et
et 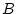 ?
?
- On suppose cette dernière condition réalisée,
et on modifie
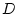 pour avoir
pour avoir 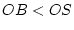 . Le plan
. Le plan 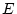 se trouve ainsi avant le passage de l'onde 2 au foyer. Ecrire
l'interférence entre les ondes 1 et 2, tracer le graphe de l'intensité
dans le plan
se trouve ainsi avant le passage de l'onde 2 au foyer. Ecrire
l'interférence entre les ondes 1 et 2, tracer le graphe de l'intensité
dans le plan 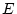 et préciser sa valeur en
et préciser sa valeur en 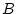 . Cette valeur dépend-elle de la position de
. Cette valeur dépend-elle de la position de 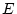 (du moment qu'on reste dans la condition
(du moment qu'on reste dans la condition 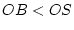 ) ?
Le centre de la figure est-il brillant ou noir ?
) ?
Le centre de la figure est-il brillant ou noir ?
- Mêmes questions dans le cas où
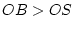 (le
plan
(le
plan 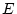 se trouve après le passage au foyer). Quelle
est alors la ``signature'' du déphasage de
se trouve après le passage au foyer). Quelle
est alors la ``signature'' du déphasage de 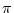 de l'amplitude
complexe lors du passage en
de l'amplitude
complexe lors du passage en 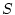 ?
?
- Sachant que le pouvoir de résolution de l'oeil est de l'ordre
de la minute d'arc et que la distance minimum de mise au point est de l'ordre
de 15 cm (un peu moins chez les jeunes), discuter l'observabilité
du phénomène dans le cadre d'une expérience classique
sur banc optique, par exemple pour des TP d'étudiants (on dipose d'un
laser émettant autour de
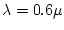 m, à vous de proposer la focale de la lentille...
cette focale doit ètre inférieure au diamètre de la
Terre).
m, à vous de proposer la focale de la lentille...
cette focale doit ètre inférieure au diamètre de la
Terre).
- On choisit maintenant une lentille convergente de focale
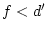 et on réalise
et on réalise 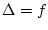 . Que se passe-t'il ?
Quelle est l'intensité dans le plan
. Que se passe-t'il ?
Quelle est l'intensité dans le plan 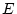 si l'on réalise
l'égalité parfaite des chemins optiques
si l'on réalise
l'égalité parfaite des chemins optiques 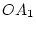 et
et 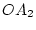 (et si on compense le déphasage global dû à
la présence de la lentille, par une lame compensatrice de même
épaisseur par exemple) ?
(et si on compense le déphasage global dû à
la présence de la lentille, par une lame compensatrice de même
épaisseur par exemple) ?
On reprend le montage précédent mais on enlève la lentille
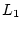 et on égalise les chemins optiques entre les deux bras
de l'interféromètre.
et on égalise les chemins optiques entre les deux bras
de l'interféromètre.
- L'onde incidente fait maintenant avec l'axe
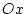 un angle
faible
un angle
faible 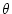 . Faire un schéma propre de ce qui
se passe et décrire la figure (intensité) observée sur
l'écran
. Faire un schéma propre de ce qui
se passe et décrire la figure (intensité) observée sur
l'écran 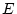 .
.
- La lumière incidente est composée de deux ondes planes
incohérentes entre elles de même longueur d'onde
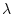 , l'une d'amplitude
, l'une d'amplitude 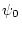 et
d'incidence normale, l'autre d'amplitude
et
d'incidence normale, l'autre d'amplitude
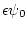 (avec
(avec 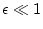 ) et d'incidence faible
) et d'incidence faible 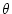 avec
l'axe
avec
l'axe 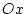 . Calculer l'intensité sur l'écran
. Calculer l'intensité sur l'écran
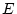 , donner le contraste de la figure.
, donner le contraste de la figure.
- On modifie très légèrement le montage : une
lentille convergente
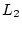 de focale
de focale 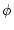 est
intercalée sur le trajet
est
intercalée sur le trajet 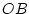 de telle sorte que
le plan
de telle sorte que
le plan 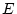 soit au foyer de cette lentille. On suppose pour
l'instant que les dimensions transversales de cette lentille sont infinies
(en d'autres termes celà revient à n'égliger les effets
de bord). Décrire la figure (intensité) observée sur
l'écran
soit au foyer de cette lentille. On suppose pour
l'instant que les dimensions transversales de cette lentille sont infinies
(en d'autres termes celà revient à n'égliger les effets
de bord). Décrire la figure (intensité) observée sur
l'écran 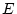 .
.
- On place à nouveau la lentille
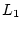 , on réalise
, on réalise
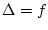 et on égalise les chemins optiques
(y compris la compensation du déphasage dû à la lentille).
Reprendre les 3 questions précédentes avec cette configuration.
Montrer que l'interposition de la lentille
et on égalise les chemins optiques
(y compris la compensation du déphasage dû à la lentille).
Reprendre les 3 questions précédentes avec cette configuration.
Montrer que l'interposition de la lentille 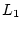 a permi d'éteindre
complètement l'onde se propageant parralèlement à l'axe
optique.
a permi d'éteindre
complètement l'onde se propageant parralèlement à l'axe
optique.
- On fait maintenant varier l'angle
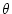 . Quelle est, en
fonction de
. Quelle est, en
fonction de 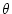 , la position et l'amplitude des pics observés
sur l'écran
, la position et l'amplitude des pics observés
sur l'écran 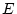 ?
?
On appelle ``nulleur'' l'ensemble constitué par l'interféromètre
de Michelson et la lentille 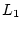 . On suppose que ce nulleur est bien
réglé (égalisation des chemins optiques et compensation
du déphasage dû à
. On suppose que ce nulleur est bien
réglé (égalisation des chemins optiques et compensation
du déphasage dû à 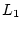 ). On désire
s'en servir pour détecter des exoplanètes et on réalise
alors le montage ci-dessous :
). On désire
s'en servir pour détecter des exoplanètes et on réalise
alors le montage ci-dessous :
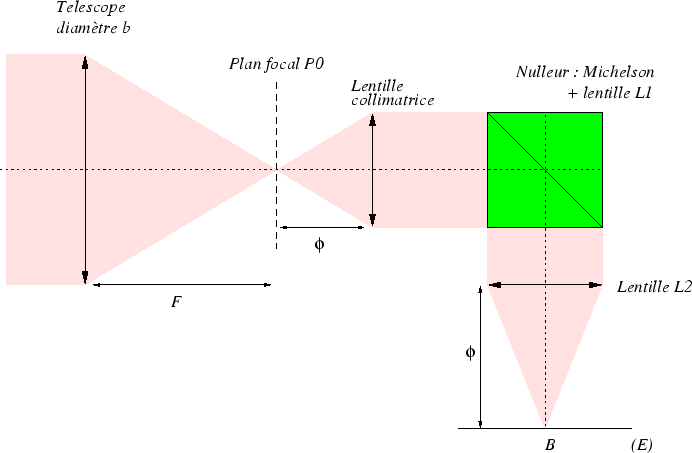
La lumière provenant des objets célestes est interceptée
par un télescope modélisé par une lentille convergente
de diamètre 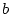 et de focale
et de focale 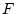 . L'image se forme au
plan focal
. L'image se forme au
plan focal 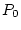 . Une seconde lentille dite ``collimatrice'',
de diamètre
. Une seconde lentille dite ``collimatrice'',
de diamètre 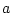 et de focale
et de focale 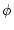 (identique à
(identique à
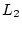 ) est placée de façon à ce que son plan
focal objet coïncide avec
) est placée de façon à ce que son plan
focal objet coïncide avec 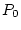 . La lumière
passe à travers le nulleur où elle est séparée
en deux parties déphasées mutuellement de
. La lumière
passe à travers le nulleur où elle est séparée
en deux parties déphasées mutuellement de 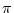 avant
de traverser la lentille
avant
de traverser la lentille 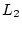 (identique à la collimatrice).
On observe sur l'écran
(identique à la collimatrice).
On observe sur l'écran 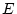 au plan focal image de
au plan focal image de 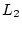 . On prendra pour les applications numériques un télescope
de diamètre 8 m, une focale de 120 m (caractéristiques
du VLT, foyer Nasmyth), un diamètre de lentille
. On prendra pour les applications numériques un télescope
de diamètre 8 m, une focale de 120 m (caractéristiques
du VLT, foyer Nasmyth), un diamètre de lentille 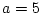 cm
et une langueur d'onde
cm
et une langueur d'onde 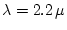 m (infrarouge, bande K).
m (infrarouge, bande K).
- Le télescope observe une étoile supposée à
l'infini. L'onde est plane et sous incidence normale en arrivant sur le télescope,
on observe à la longueur d'onde
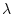 . Décrire
l'image (intensité)
. Décrire
l'image (intensité) 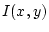 dans le plan
dans le plan 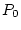 . Tracer
en échelle logarithmique le graphe de
. Tracer
en échelle logarithmique le graphe de 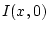 et donner les
rapports des maxima secondaires au maximum principal.
et donner les
rapports des maxima secondaires au maximum principal.
- Une planète se trouve à côté de l'étoile.
L'onde plane arrive sur le télescope avec un faible angle d'incidence
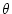 . Le rapport des amplitudes planète/étoile
est
. Le rapport des amplitudes planète/étoile
est 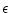 . Les deux ondes sont incohérentes
entre elles, la situation est identique à celle de la question 2-2.
Décrire l'image (intensité) dans le plan
. Les deux ondes sont incohérentes
entre elles, la situation est identique à celle de la question 2-2.
Décrire l'image (intensité) dans le plan 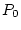 dans
le cas où les deux images produites par l'étoile et sa planète
sont bien séparées. Tracez l'intensité en échelle
logarithmique pour
dans
le cas où les deux images produites par l'étoile et sa planète
sont bien séparées. Tracez l'intensité en échelle
logarithmique pour 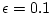 .
.
- On suppose que la planète est détectable si l'intensité
maximale qu'elle produit dans l'image est supérieure ou égale
à l'intensité du premier maximum secondaire de la tache d'Airy
correspondant à l'image de l'étoile. Quel est alors le plus
grand rapport d'intensité détectable entre la planète
et son compagnon ? Un rapport de
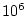 vous semble-il détectable ?
vous semble-il détectable ?
- L'étoile est seule, la situation est identique à celle
de la question 3.1-1. Décrire l'onde à la sortie de la collimatrice.
Cette collimatrice étant de diamètre
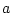 , quelle
doit ètre la valeur maximum de sa focale
, quelle
doit ètre la valeur maximum de sa focale 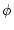 pour
qu'elle ne diaphragme pas l'onde lumineuse incidente ? Que vaut l'intensité
dans le plan
pour
qu'elle ne diaphragme pas l'onde lumineuse incidente ? Que vaut l'intensité
dans le plan 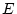 .
.
- Que vaut l'intesité dans le plan
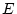 dans le
cas où la planète est seule ?
dans le
cas où la planète est seule ?
- Ecrire l'intensité totale observée dans le plan
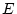 lorsque le télescope observe l'ensemble planète+étoile.
Discuter le potentiel de ce dispositif pour détecter des exoplanètes.
lorsque le télescope observe l'ensemble planète+étoile.
Discuter le potentiel de ce dispositif pour détecter des exoplanètes.
- En utilisant le critère de Rayleigh, donner l'angle
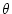 minimal détectable. Faites l'application numérique
avec les valeurs proposées plus haut et discuter l'observabilité
des planètes de 51 Peg (vous chercherez les données dans
la littérature).
minimal détectable. Faites l'application numérique
avec les valeurs proposées plus haut et discuter l'observabilité
des planètes de 51 Peg (vous chercherez les données dans
la littérature).
- On cherche maintenant à étudier l'effet d'un mauvais
centrage de l'étoile sur l'axe optique (une erreur de guidage par
exemple). L'onde provenant de l'étoile arrive ainsi avec un angle
d'incidence
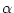 faible, l'incidence de l'onde provenant
de la planète étant
faible, l'incidence de l'onde provenant
de la planète étant 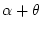 . Que se
passe-t'il ? Ecrire l'intensité dans le plan
. Que se
passe-t'il ? Ecrire l'intensité dans le plan 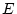 . Quel est
le décentrage
. Quel est
le décentrage 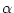 maximum acceptable pour qu'on
puisse encore détecter une planète
maximum acceptable pour qu'on
puisse encore détecter une planète 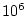 fois
plus faible que l'étoile (rapport des intensités) ?
fois
plus faible que l'étoile (rapport des intensités) ?
![]() ) mais encore hors
de portée des techniques actuelles... ou en tout cas d'il y a quelques
années puisqu'un nouveau champ de recherches dans l'imagerie à
très haute dynamique est apparu il y a peu. L'idée centrale
de ces techniques est d'éteindre la lumière provenant de l'étoile
pour faire ressortir celle de la planète. Les solutions techniques
s'orientent vers deux voies : le nulling, ou extinction par
interférence destructice, et la coronographie basée sur une
occulation par des masques adaptés. L'objectif de ce problème
est de faire une étude de principe de l'un de ces instruments, le
``Coronographe Interférentiel Achromatique'', développé
à l'observatoire de la Côte d'Azur par l'équipe de Jean
Gay.
) mais encore hors
de portée des techniques actuelles... ou en tout cas d'il y a quelques
années puisqu'un nouveau champ de recherches dans l'imagerie à
très haute dynamique est apparu il y a peu. L'idée centrale
de ces techniques est d'éteindre la lumière provenant de l'étoile
pour faire ressortir celle de la planète. Les solutions techniques
s'orientent vers deux voies : le nulling, ou extinction par
interférence destructice, et la coronographie basée sur une
occulation par des masques adaptés. L'objectif de ce problème
est de faire une étude de principe de l'un de ces instruments, le
``Coronographe Interférentiel Achromatique'', développé
à l'observatoire de la Côte d'Azur par l'équipe de Jean
Gay.
![]() et
et ![]() une lentille convergente
une lentille convergente
![]() de focale
de focale ![]() . Cette lentille est placée
à une distance
. Cette lentille est placée
à une distance ![]() de
de ![]() . On éclaire
l'ensemble par une onde plane monochromatique de longueur d'onde
. On éclaire
l'ensemble par une onde plane monochromatique de longueur d'onde ![]() provenant de la gauche de la figure et se propageant dans
le sens des
provenant de la gauche de la figure et se propageant dans
le sens des ![]() . On se place dans les conditions de l'otique
paraxiale et on négligera les effets de diffraction par les bords
des mitoirs et de la lentille (ce qui revient à considérer
ceux-ci comme infinis).
. On se place dans les conditions de l'otique
paraxiale et on négligera les effets de diffraction par les bords
des mitoirs et de la lentille (ce qui revient à considérer
ceux-ci comme infinis). 
![]() et de focale
et de focale ![]() . L'image se forme au
plan focal
. L'image se forme au
plan focal ![]() . Une seconde lentille dite ``collimatrice'',
de diamètre
. Une seconde lentille dite ``collimatrice'',
de diamètre ![]() et de focale
et de focale ![]() (identique à
(identique à
![]() ) est placée de façon à ce que son plan
focal objet coïncide avec
) est placée de façon à ce que son plan
focal objet coïncide avec ![]() . La lumière
passe à travers le nulleur où elle est séparée
en deux parties déphasées mutuellement de
. La lumière
passe à travers le nulleur où elle est séparée
en deux parties déphasées mutuellement de ![]() avant
de traverser la lentille
avant
de traverser la lentille ![]() (identique à la collimatrice).
On observe sur l'écran
(identique à la collimatrice).
On observe sur l'écran ![]() au plan focal image de
au plan focal image de ![]() . On prendra pour les applications numériques un télescope
de diamètre 8 m, une focale de 120 m (caractéristiques
du VLT, foyer Nasmyth), un diamètre de lentille
. On prendra pour les applications numériques un télescope
de diamètre 8 m, une focale de 120 m (caractéristiques
du VLT, foyer Nasmyth), un diamètre de lentille ![]() cm
et une langueur d'onde
cm
et une langueur d'onde ![]() m (infrarouge, bande K).
m (infrarouge, bande K).