L'équation de propagation de
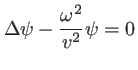
avec le laplacien réduit à sa partie radiale qui s'écrit
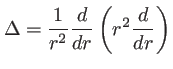
en introduisant le vecteur d'onde
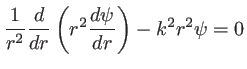
Le chamgement de variable
dont la solution en
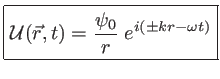 |
(1.10) |
|
Signe -
les surfaces d'onde se propagent vers 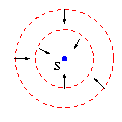 
|
|
Signe +
les surfaces d'onde se propagent vers 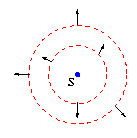 
|
On peut noter deux différences avec l'écriture de l'onde plane
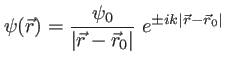 |
(1.11) |