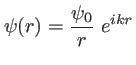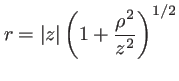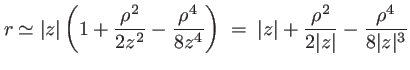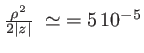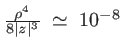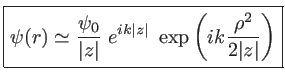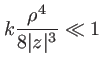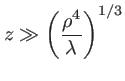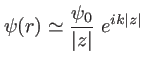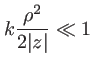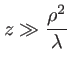On considère une onde shérique dont la source est en 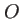 , on cherche à exprimer son amplitude complexe en un point
, on cherche à exprimer son amplitude complexe en un point 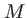 de coordonnées
de coordonnées 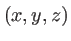 avec la condition
avec la condition
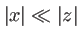 et
et
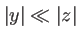 (point proche de l'axe : les rayons provenant de la source sont peu inclinés en
(point proche de l'axe : les rayons provenant de la source sont peu inclinés en 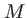 ). On supposera que l'onde est divergente (signe +) dans l'exponentielle. Il suffira de changer
). On supposera que l'onde est divergente (signe +) dans l'exponentielle. Il suffira de changer 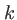 en
en 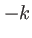 dans les expressions qui vont suivre pour une onde convergente.
dans les expressions qui vont suivre pour une onde convergente.
L'amplitude complexe en 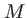 est
est
avec
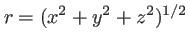 . Notons
. Notons
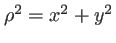 , on a
, on a
puisque
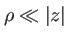 on fait un développement limité de
on fait un développement limité de 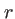
Pour savoir à quel ordre on peut stopper le développement limité, il faut prendre des hypothèses sur les valeurs de 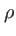 ,
, 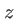 et
et 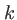 . Prenons les valeurs
. Prenons les valeurs
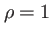 cm,
cm, 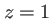 m, et
m, et 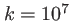 m
m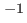 (lumière visible). Les trois termes intervenant dans le développement de
(lumière visible). Les trois termes intervenant dans le développement de 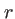 valent
valent
- terme (1) :
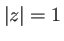
- terme (2) :
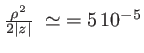
- terme (3) :
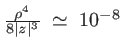
On pourrait ainsi se contenter du premier terme en posant simplement 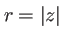 , qui donne une erreur à la cinquième décimale. Cette approximation est suffisante pour le terme
, qui donne une erreur à la cinquième décimale. Cette approximation est suffisante pour le terme 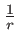 qui intervient devant l'exponentielle complexe. Mais pas pour le terme
qui intervient devant l'exponentielle complexe. Mais pas pour le terme 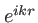 à cause de la grande valeur de
à cause de la grande valeur de 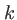 et il est nécessaire, à l'intérieur de l'exponentielle, de garder les deux premiers termes (le 3e peut par contre être négligé). Ainsi, une onde sphérique dans l'approximation paraxiale s'écrira :
et il est nécessaire, à l'intérieur de l'exponentielle, de garder les deux premiers termes (le 3e peut par contre être négligé). Ainsi, une onde sphérique dans l'approximation paraxiale s'écrira :
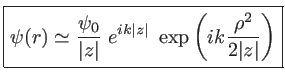 |
(1.12) |
Dans un plan 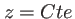 , on voit que la phase de l'onde est en
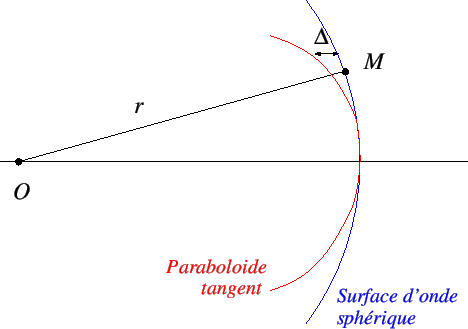
, on voit que la phase de l'onde est en 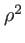 , la surface d'onde est un paraboloïde. Il s'agit du paraboloïde tangent à la sphère au point
, la surface d'onde est un paraboloïde. Il s'agit du paraboloïde tangent à la sphère au point 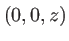 , on parle de paraboloïde osculateur (même courbure que la sphère), voir figure 1.2.
, on parle de paraboloïde osculateur (même courbure que la sphère), voir figure 1.2.
Fig. 1.2:
Surface d'onde d'une onde sphérique et son approximation paraxiale, le paraboloïde tangent. L'écart 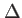 entre les deux surfaces est
entre les deux surfaces est
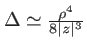 , terme du 3e ordre du développement limité de
, terme du 3e ordre du développement limité de 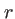 .
.
 |
Il faut que 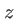 soit assez grand pour pouvoir négliger l'ordre 3 du développement limité de
soit assez grand pour pouvoir négliger l'ordre 3 du développement limité de 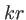 , donc que
, donc que
ce qui donne
Avec les valeurs numériques 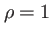 cm et
cm et
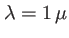 m, on obtient la condition
m, on obtient la condition 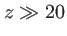 cm.
cm.
Lorsque 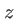 devient assez grand, on pourra négliger aussi le second ordre du développement limité de
devient assez grand, on pourra négliger aussi le second ordre du développement limité de 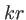 . Dans ce cas l'amplitude complexe de l'onde s'écrit :
. Dans ce cas l'amplitude complexe de l'onde s'écrit :
c'est à dire une onde plane, dont les surfaces d'onde sont des sphères de rayon de courbure assez grand pour les approximer par leur plan tangent. On parle alors de champ lointain, et cette approximation de l'onde sphérique par une onde plane conduit à la diffraction de Fraunofer ou diffraction à l'infini, qui sera abordée plus loin. Celà se produit lorsque
c'est à dire
Avec les valeurs numériques 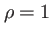 cm et
cm et
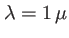 m, on obtient la condition
m, on obtient la condition 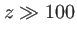 m.
m.
![]() est
est