Soit une onde plane (monochromatique) d'amplitude complexe
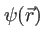 de vecteur d'onde
de vecteur d'onde 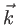 quelconque, se propageant vers les
quelconque, se propageant vers les 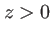 . L'espace est repéré par un système d'axes
. L'espace est repéré par un système d'axes 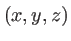 ,
, 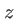 étant l'axe optique. On note :
étant l'axe optique. On note :
Cette notation fait bien ressortir le fait que 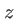 est ici un paramètre et que les amplitudes
est ici un paramètre et que les amplitudes 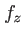 sont des fonctions bidimensionnelles. Si
sont des fonctions bidimensionnelles. Si
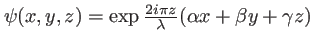 , il est trivial de voir que :
, il est trivial de voir que :
![$\displaystyle f_{z_2}(x,y)=f_{z_1}(x,y)\; \exp\left[\frac{2i\pi\gamma (z_2-z_1)}{\lambda}\right]$](img188.png) |
(1.13) |
Un onde plane qui se propage d'un plan 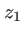 à un plan
à un plan 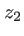 subit donc un simple déphasage. Ce ne sera pas le cas pour les autres types ondes dont on va montrer qu'elles subissent une transformation plus compliquée qu'un simple déphasage.
subit donc un simple déphasage. Ce ne sera pas le cas pour les autres types ondes dont on va montrer qu'elles subissent une transformation plus compliquée qu'un simple déphasage.
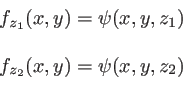
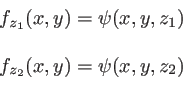
![$\displaystyle f_{z_2}(x,y)=f_{z_1}(x,y)\; \exp\left[\frac{2i\pi\gamma (z_2-z_1)}{\lambda}\right]$](img188.png)