Propagation d'une somme discrète d'ondes planes
On considère une somme discrète de 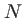 ondes planes monochromatiques ayant toutes la même
pulsation
ondes planes monochromatiques ayant toutes la même
pulsation 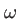 et dont les champs électriques sont parallèles. Les vecteurs d'onde seront notés
et dont les champs électriques sont parallèles. Les vecteurs d'onde seront notés 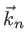 de composantes
de composantes
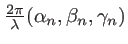 . L'amplitude complexe s'écrit :
. L'amplitude complexe s'écrit :
Nous cherchons à dégager la relation qui existe entre les valeurs de l'amplitude dans deux
plans 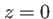 et
et 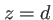 (transformée de Fresnel de
(transformée de Fresnel de 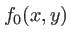 sur une distance
sur une distance 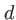 ). Nous savons écrire
cette relation dans le cas d'une onde plane ; en utilisant le principe de superposition
linéaire des champs électriques, il vient que l'amplitude en
). Nous savons écrire
cette relation dans le cas d'une onde plane ; en utilisant le principe de superposition
linéaire des champs électriques, il vient que l'amplitude en 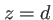 de la somme d'ondes planes
est la somme des amplitudes complexes de chacune des ondes planes en
de la somme d'ondes planes
est la somme des amplitudes complexes de chacune des ondes planes en 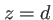 .
Nous connaissons l'expression de l'onde en
.
Nous connaissons l'expression de l'onde en 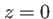 :
:
![$\displaystyle f_0(x,y)=\sum_{n=1}^{N} A_n \exp \left[\frac{2i\pi}{\lambda}(\alpha_n x+\beta_n y)\right]$](img196.png) |
(1.14) |
on effectue la propagation individuelle de chaque onde plane : celà consiste à
multiplier chaque terme de la somme par
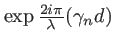 . On
fait ensuite la somme pour obtenir l'expression de l'amplitude de l'onde en
. On
fait ensuite la somme pour obtenir l'expression de l'amplitude de l'onde en 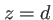 :
:
![$\displaystyle f_d(x,y)=\sum_{n=1}^{N} A_n \exp \left[\frac{2i\pi}{\lambda}(\alpha_n x+\beta_n y+\gamma_n d)\right]$](img198.png) |
(1.15) |
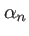 et
et 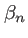 sont connus si l'on connait
sont connus si l'on connait 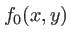 ,
, 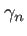 ne l'est pas mais
peut être obtenu par la relation
ne l'est pas mais
peut être obtenu par la relation
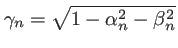 .
.
![$\displaystyle \psi(x,y,z)=f_z(x,y) = \; \sum_{n=1}^{N} A_n \exp\left[ \frac{2i\pi}{\lambda}(\alpha_n x+\beta_n y+\gamma_n z)\right]
$](img194.png)
![$\displaystyle \psi(x,y,z)=f_z(x,y) = \; \sum_{n=1}^{N} A_n \exp\left[ \frac{2i\pi}{\lambda}(\alpha_n x+\beta_n y+\gamma_n z)\right]
$](img194.png)
![]() et
et ![]() (transformée de Fresnel de
(transformée de Fresnel de ![]() sur une distance
sur une distance ![]() ). Nous savons écrire
cette relation dans le cas d'une onde plane ; en utilisant le principe de superposition
linéaire des champs électriques, il vient que l'amplitude en
). Nous savons écrire
cette relation dans le cas d'une onde plane ; en utilisant le principe de superposition
linéaire des champs électriques, il vient que l'amplitude en ![]() de la somme d'ondes planes
est la somme des amplitudes complexes de chacune des ondes planes en
de la somme d'ondes planes
est la somme des amplitudes complexes de chacune des ondes planes en ![]() .
Nous connaissons l'expression de l'onde en
.
Nous connaissons l'expression de l'onde en ![]() :
:
![$\displaystyle f_d(x,y)=\sum_{n=1}^{N} A_n \exp \left[\frac{2i\pi}{\lambda}(\alpha_n x+\beta_n y+\gamma_n d)\right]$](img198.png)