Prenons l'exemple d'une onde plane de longueur d'onde
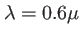 m qui traverse un petit diaphragme de rayon
m qui traverse un petit diaphragme de rayon 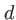 mm situé dans le plan
mm situé dans le plan 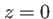 . Nous allons déterminer la valeur de
. Nous allons déterminer la valeur de 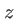 à partir de laquelle l'approximation de Fraunhofer donne une erreur faible sur la valeur de l'amplitude complexe.
à partir de laquelle l'approximation de Fraunhofer donne une erreur faible sur la valeur de l'amplitude complexe.
Cette approximation consiste à égaler à 1 le terme
présent dans la transformée de Fresnel. Au premier ordre en 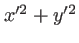 il vient :
il vient :
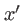 et
et 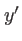 sont des variables d'intégration dans le plan du diaphragme et vérifient
sont des variables d'intégration dans le plan du diaphragme et vérifient
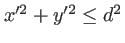 . L'erreur
. L'erreur 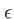 commise dans l'approximation de Fraunhofer est donc :
commise dans l'approximation de Fraunhofer est donc :
la valeur de 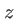 telle que cette erreur
telle que cette erreur
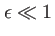 doit donc vérifier
doit donc vérifier
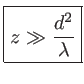 |
(1.31) |
Avec 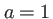 cm et
cm et
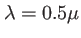 m, on obtient
m, on obtient 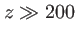 mètres. Deux problèmes techniques se posent alors pour réaliser une ``bonne'' expérience de diffraction à l'infini :
mètres. Deux problèmes techniques se posent alors pour réaliser une ``bonne'' expérience de diffraction à l'infini :
- Un problème d'encombrement du montage optique au vu des distances nécessaires
- Un problème de luminosité, l'amplitude décroissant comme
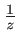 et l'intensité comme
et l'intensité comme
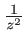 . Dans l'exemple ci-dessus la figure de diffraction de Fraunhofer serait
. Dans l'exemple ci-dessus la figure de diffraction de Fraunhofer serait 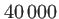 fois moins lumineuse que l'onde dans le plan du diaphragme.
fois moins lumineuse que l'onde dans le plan du diaphragme.
On verra par la suite que l'on peut quand même réaliser une diffraction à l'infini sur des distances raisonnables en observant dans le plan focal d'une lentille convergente.
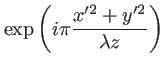
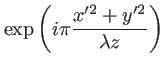
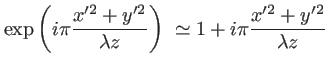
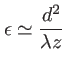
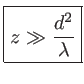
![]() cm et
cm et
![]() m, on obtient
m, on obtient ![]() mètres. Deux problèmes techniques se posent alors pour réaliser une ``bonne'' expérience de diffraction à l'infini :
mètres. Deux problèmes techniques se posent alors pour réaliser une ``bonne'' expérience de diffraction à l'infini :