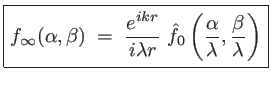Ecrivons l'expression du principe de Huyghens-Fresnel entre les amplitudes
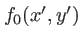 et
et 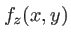 :
:
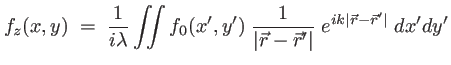 |
(1.32) |
où
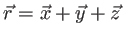 est la position du point courant et
est la position du point courant et
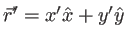 celle d'un point dans le plan
celle d'un point dans le plan 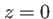 . Faisons tendre
. Faisons tendre
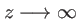 , il vient
, il vient
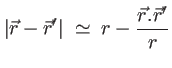 |
(1.33) |
c'est une onde sphérique et l'approximation peut être faite à l'ordre zéro au dénominateur. On écrit :
alors que le terme intervenant dans l'exponentielle doit être développé à l'odre suivant à cause du vecteur d'onde 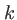 qui peut être grand (de l'ordre de
qui peut être grand (de l'ordre de 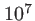 en lumière visible). Il vient :
en lumière visible). Il vient :
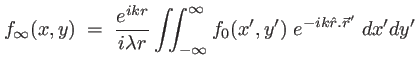 |
(1.34) |
Introduisons les coordonnées du vecteur unitaire
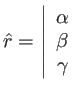 On obtient là encore l'expression d'une transformée de Fourier :
On obtient là encore l'expression d'une transformée de Fourier :
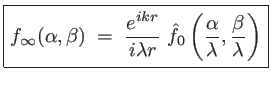 |
(1.35) |
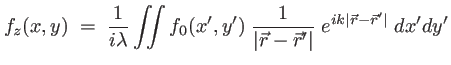
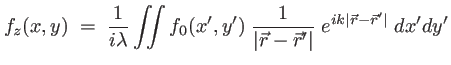
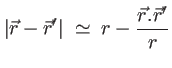
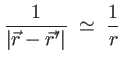
![]() qui peut être grand (de l'ordre de
qui peut être grand (de l'ordre de ![]() en lumière visible). Il vient :
en lumière visible). Il vient :
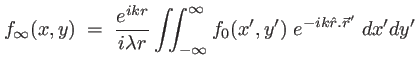
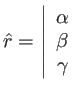 On obtient là encore l'expression d'une transformée de Fourier :
On obtient là encore l'expression d'une transformée de Fourier :