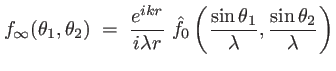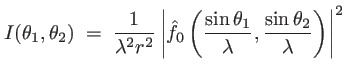Le vecteur unitaire  définit une direction dans le demi-espace
définit une direction dans le demi-espace  . Cette direction ne dépend que de
. Cette direction ne dépend que de 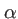 et
et 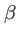 puisque la valeur de
puisque la valeur de 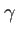 est fixée par
est fixée par
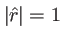 . On peut introduire des angles
. On peut introduire des angles 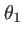 et
et 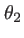 tels que :
tels que :
ces angles, lorsqu'ils sont faibles, s'identifient aux coordonnées sphériques 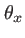 et
et 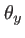 définies au début du chapitre. On peut ainsi écrire l'amplitude diffractée dans la direction d'angles
définies au début du chapitre. On peut ainsi écrire l'amplitude diffractée dans la direction d'angles
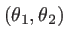 :
:
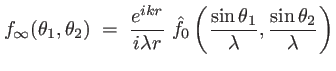 |
(1.36) |
L'intensité est donnée par
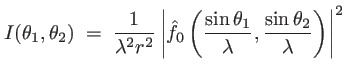 |
(1.37) |
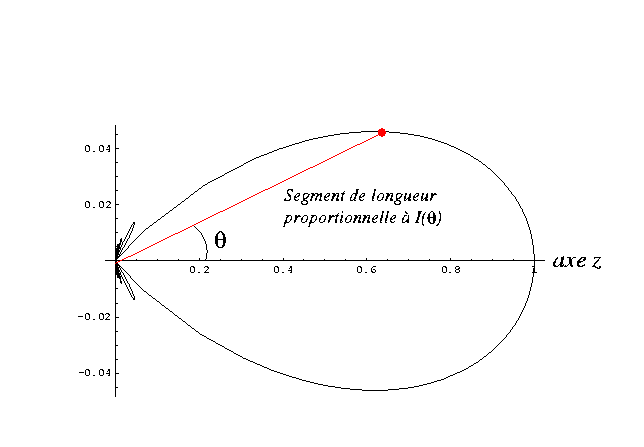
Fig. 1.5:
La courbe ci-dessus montre l'indicatrice de diffraction dans le plan 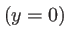 pour la lumière diffractée par une fente rectangulaire, éclairée en incidence normale. On note un maximum d'intensité diffractée sur l'axe, puis des petits lobes secondaires; la figure est décrite par un sinus cardinal carré; (voir paragraphe 1.8.1.
pour la lumière diffractée par une fente rectangulaire, éclairée en incidence normale. On note un maximum d'intensité diffractée sur l'axe, puis des petits lobes secondaires; la figure est décrite par un sinus cardinal carré; (voir paragraphe 1.8.1.
 |
Lorque 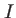 est à symétrie de révolution autour de l'axe
est à symétrie de révolution autour de l'axe 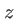 (les deux angles
(les deux angles 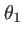 et
et 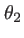 sont équivalents), on représente parfois cette fonction en coordonnées polaires sous la forme d'une courbe ; la distance entre l'origine du repère et l'extrémité de la courbe est proportionnelle à
sont équivalents), on représente parfois cette fonction en coordonnées polaires sous la forme d'une courbe ; la distance entre l'origine du repère et l'extrémité de la courbe est proportionnelle à 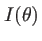 (voir figure 1.5). Cette courbe appelée indicatrice de diffraction ressemble aux diagrammes de rayonnement des antennes. Si l'intensité n'est pas à symétrie de révolution, cette courbe est une surface.
(voir figure 1.5). Cette courbe appelée indicatrice de diffraction ressemble aux diagrammes de rayonnement des antennes. Si l'intensité n'est pas à symétrie de révolution, cette courbe est une surface.