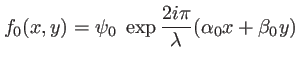 |
(1.38) |
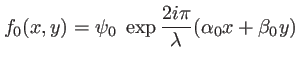 |
(1.38) |
L'amplitude diffractée à l'infini s'écrit
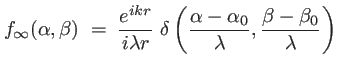 |
(1.39) |
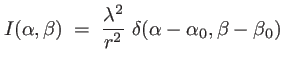 |
(1.40) |

 .
.
On notera qu'il est impossible dans le cas d'une onde plane de trouver une distance ![]() assez grande pour pouvoir faire l'approximation de Fraunofer puisque l'extension spatiale de cette onde dans le plan
assez grande pour pouvoir faire l'approximation de Fraunofer puisque l'extension spatiale de cette onde dans le plan ![]() est infinie.
est infinie.