Sont concernés les prismes, lentilles, certains types de réseaux de diffraction, les lames de verre, etc...Ce sont généralement des écrans qui
- ont un indice de réfraction dépendant de la position (ex: bulles de gaz, atmosphère turbulente...)
- ont un indice fixe, différent de celui du milieu environnant, et dont l'épaisseur est fonction de la position (ex: prisme ou lentille)
On s'intéressera au second cas dans l'hypothèse où l'épaisseur des écrans est faible (écrans minces).
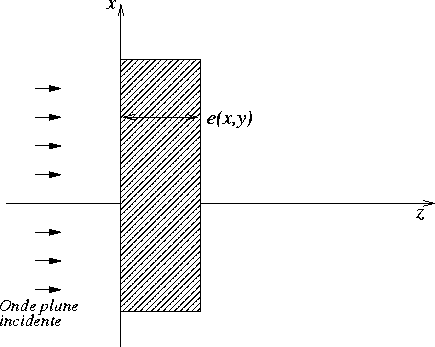
Fig. 1.8:
Ecran transparent d'indice 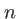 et d'épaisseur
et d'épaisseur 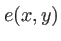 . Cet écran possède un coefficient de transmission
. Cet écran possède un coefficient de transmission
![$ t(x,y)=\exp\left[\frac{2i\pi}{\lambda}(n-1)e(x,y)\right]$](img322.png) .
.
|
On se place dans les conditions de la figure 1.8. Le plan d'entrée du masque est le plan 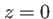 . La fonction épaisseur du masque est
. La fonction épaisseur du masque est 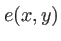 . Elle est supposée faible (écrans minces) et on supposera aussi qu'on se trouve dans les conditions paraxiales (inclinaisons faibles).
Ce masque est éclairé par une onde plane sous incidence normale se propageant dans la direction des
. Elle est supposée faible (écrans minces) et on supposera aussi qu'on se trouve dans les conditions paraxiales (inclinaisons faibles).
Ce masque est éclairé par une onde plane sous incidence normale se propageant dans la direction des 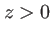 . On note
. On note 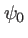 l'amplitude de l'onde dans le plan
l'amplitude de l'onde dans le plan 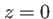 ,
, 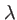 sa longueur d'onde et on désigne par
sa longueur d'onde et on désigne par 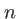 l'indice du matériau composant le masque. Cet indice est supposé constant.
l'indice du matériau composant le masque. Cet indice est supposé constant.
Considérons un point 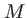 situé à la position
situé à la position 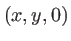 dans le plan d'entrée du masque. Après propagation dans le matériau, l'onde en sort au point
dans le plan d'entrée du masque. Après propagation dans le matériau, l'onde en sort au point 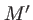 de coordonnées
de coordonnées 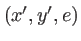 à la sortie du masque. Si on néglige les inclinaisons, et puisque
à la sortie du masque. Si on néglige les inclinaisons, et puisque 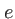 est faible, les coordonnées transverses de
est faible, les coordonnées transverses de 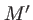 sont les mêmes que celles de
sont les mêmes que celles de 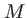 , c'est à dire
, c'est à dire 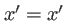 et
et 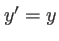 . L'onde en
. L'onde en 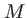 s'écrit :
s'écrit :
l'onde en 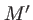 s'écrit
s'écrit
où
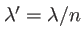 est la longueur d'onde de la lumière dans le matériau.
Si l'onde s'était propagée librement de
est la longueur d'onde de la lumière dans le matériau.
Si l'onde s'était propagée librement de 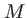 à
à 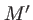 en l'absence du masque, son amplitude en
en l'absence du masque, son amplitude en 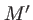 aurait été
aurait été
L'effet du masque sur la propagation de l'onde est de transformer 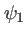 en
en 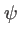 en introduisant le facteur multiplicatif
en introduisant le facteur multiplicatif
![$\displaystyle \mbox{\fbox{$\displaystyle t(x,y)=\frac{\psi(x,y,e)}{\psi_1(x,y,e)}=\exp\left[\frac{2i\pi}{\lambda}(n-1)e(x,y)\right] $}}$](img335.png) |
(1.44) |
Pour tout 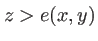 , le masque se comporte alors comme un écran plat, situé dans le plan
, le masque se comporte alors comme un écran plat, situé dans le plan 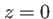 et de coefficient de transmission
et de coefficient de transmission 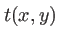 . On remarque que dans ce cas
. On remarque que dans ce cas
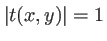 et que le masque n'agit que sur la phase de l'onde et pas sur son amplitude. D'où le nom d'écran de phase donné à ce type de masque.
et que le masque n'agit que sur la phase de l'onde et pas sur son amplitude. D'où le nom d'écran de phase donné à ce type de masque.


![]() . La fonction épaisseur du masque est
. La fonction épaisseur du masque est ![]() . Elle est supposée faible (écrans minces) et on supposera aussi qu'on se trouve dans les conditions paraxiales (inclinaisons faibles).
Ce masque est éclairé par une onde plane sous incidence normale se propageant dans la direction des
. Elle est supposée faible (écrans minces) et on supposera aussi qu'on se trouve dans les conditions paraxiales (inclinaisons faibles).
Ce masque est éclairé par une onde plane sous incidence normale se propageant dans la direction des ![]() . On note
. On note ![]() l'amplitude de l'onde dans le plan
l'amplitude de l'onde dans le plan ![]() ,
, ![]() sa longueur d'onde et on désigne par
sa longueur d'onde et on désigne par ![]() l'indice du matériau composant le masque. Cet indice est supposé constant.
l'indice du matériau composant le masque. Cet indice est supposé constant.
![]() situé à la position
situé à la position ![]() dans le plan d'entrée du masque. Après propagation dans le matériau, l'onde en sort au point
dans le plan d'entrée du masque. Après propagation dans le matériau, l'onde en sort au point ![]() de coordonnées
de coordonnées ![]() à la sortie du masque. Si on néglige les inclinaisons, et puisque
à la sortie du masque. Si on néglige les inclinaisons, et puisque ![]() est faible, les coordonnées transverses de
est faible, les coordonnées transverses de ![]() sont les mêmes que celles de
sont les mêmes que celles de ![]() , c'est à dire
, c'est à dire ![]() et
et ![]() . L'onde en
. L'onde en ![]() s'écrit :
s'écrit :
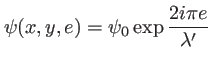
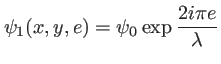
![$\displaystyle \mbox{\fbox{$\displaystyle t(x,y)=\frac{\psi(x,y,e)}{\psi_1(x,y,e)}=\exp\left[\frac{2i\pi}{\lambda}(n-1)e(x,y)\right] $}}$](img335.png)