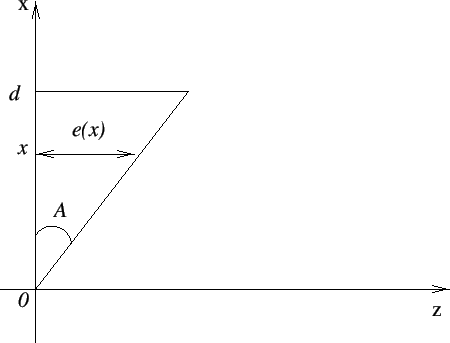
Fig. 1.9:
Prisme d'angle au sommet 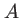 . L'épaisseur de verre traversée par un rayon arrivant en un point d'abcisse
. L'épaisseur de verre traversée par un rayon arrivant en un point d'abcisse 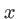 est
est
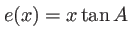
 |
On se place dans les conditions de la figure 1.9. Le prisme d'indice 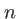 a un angle au sommet
a un angle au sommet 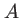 . Ce prisme est considéré infini dans la direction
. Ce prisme est considéré infini dans la direction 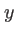 et de hauteur
et de hauteur 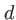 dans la direction
dans la direction 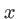 . L'épaisseur de verre est fonction de
. L'épaisseur de verre est fonction de 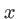 et s'écrit :
et s'écrit :
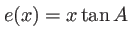 |
(1.45) |
et le prisme est limité spatialement entre les valeurs 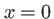 et
et 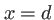 , on a donc
, on a donc
 |
(1.46) |
et on écrit finalement
![$\displaystyle t(x,y)=\prod\left( \frac{x-d/2}{d}\right) \; \exp\left[ \frac{2i\pi}{\lambda}(n-1)x \tan A\right]\; 1\!\!$](img344.png) 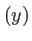 |
(1.47) |
la fonction 1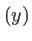 est la fonction qui vaut 1
quel que soit
est la fonction qui vaut 1
quel que soit 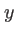 . Son écriture explicite permet d'éviter d'oublier la dépendance en
. Son écriture explicite permet d'éviter d'oublier la dépendance en 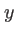 lors des calculs (apparition d'un
lors des calculs (apparition d'un 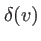 lors d'une T.F. par exemple).
lors d'une T.F. par exemple).
Dans le cas d'un prisme infini dans la direction 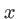 éclairé sous incidence normale (amplitude
éclairé sous incidence normale (amplitude 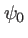 dans le plan d'entrée du prisme), l'onde sortant du prisme s'écrit dans le plan
dans le plan d'entrée du prisme), l'onde sortant du prisme s'écrit dans le plan 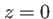 :
:
c'est l'amplitude d'une onde plane de direction
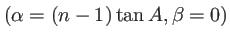 . On retrouve un résultat connu en optique géométrique (déviation d'une onde plane par un prisme).
. On retrouve un résultat connu en optique géométrique (déviation d'une onde plane par un prisme).



![$\displaystyle t(x,y)=\prod\left( \frac{x-d/2}{d}\right) \; \exp\left[ \frac{2i\pi}{\lambda}(n-1)x \tan A\right]\; 1\!\!$](img344.png)
![]() éclairé sous incidence normale (amplitude
éclairé sous incidence normale (amplitude ![]() dans le plan d'entrée du prisme), l'onde sortant du prisme s'écrit dans le plan
dans le plan d'entrée du prisme), l'onde sortant du prisme s'écrit dans le plan ![]() :
:
![$\displaystyle \psi(x,y,z=0^+)=\psi_0 \; \exp \frac{2i\pi}{\lambda}\left[(n-1)\tan A\right]x
$](img350.png)