Fig. 1.10:
Lentille convergente plan-convexe. L'épaisseur de verre traversée par un rayon arrivant en un point de coordonnées 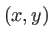 dans dans le plan d'entrée de la lentille est
dans dans le plan d'entrée de la lentille est
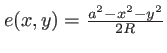 .
.
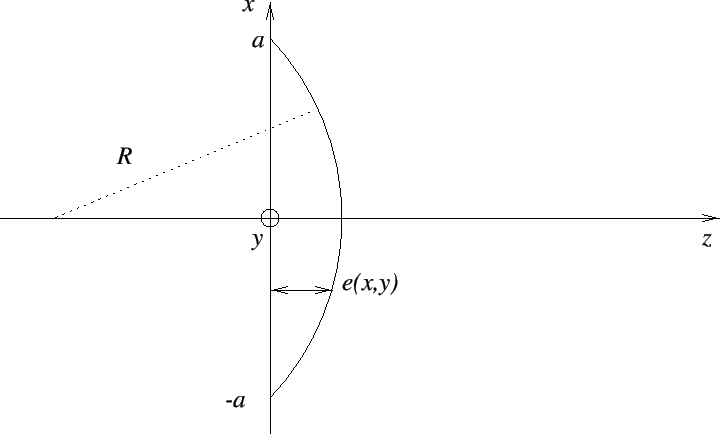 |
On considère le lentille plan-convexe de la figure 1.10, la face plate définissant le plan 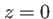 . Le rayon de courbure de la face bombée est
. Le rayon de courbure de la face bombée est 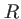 , le diamètre de la lentille est
, le diamètre de la lentille est 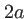 . On suppose
. On suppose 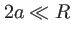 et on note
et on note 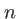 l'indice du verre composant le lentille.
l'indice du verre composant le lentille.
Un point 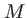 appartenant à la surface bombée possède des coordonnées qui vérifient l'équation de la sphère. Le centre de la sphère se trouve en
appartenant à la surface bombée possède des coordonnées qui vérifient l'équation de la sphère. Le centre de la sphère se trouve en
et l'équation de la sphère s'écrit :
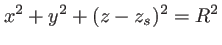 |
(1.48) |
soit
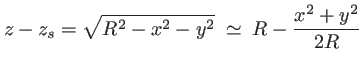 |
(1.49) |
donc
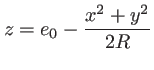 |
(1.50) |
et pour trouver 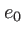 on peut remarquer que lorsque
on peut remarquer que lorsque
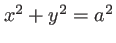 l'épaisseur de verre traversée est nulle (on se trouve au bord de la lentille) ; il vient:
l'épaisseur de verre traversée est nulle (on se trouve au bord de la lentille) ; il vient:
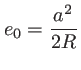 |
(1.51) |
la fonction épaisseur  est égale à la coordonnée
est égale à la coordonnée 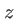 du point
du point 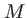 , d'où le coefficient de transmission de la lentille convergente :
, d'où le coefficient de transmission de la lentille convergente :
![$\displaystyle t(x,y)=e^{\frac{i\pi a^2 (n-1)}{\lambda R}}\; \exp\left[-\frac{i\pi (x^2+y^2)}{\lambda R} (n-1) \right]$](img363.png) |
(1.52) |
Le terme constant dépendant de 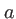 traduit le déphasage que subit le rayon passant par l'axe optique à la traversée de la lentille. Souvent on omettra ce terme constant, pour écrire le coefficient de transmission de la lentille convergente comme suit
traduit le déphasage que subit le rayon passant par l'axe optique à la traversée de la lentille. Souvent on omettra ce terme constant, pour écrire le coefficient de transmission de la lentille convergente comme suit
![$\displaystyle \mbox{\fbox{$\displaystyle t(x,y)=\exp\left[-\frac{i\pi (x^2+y^2)}{\lambda R} (n-1) \right] $}}$](img364.png) |
(1.53) |
C'est l'amplitude d'une onde sphérique convergente (signe - dans l'exponentielle) dont le centre se trouve en
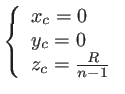 |
(1.54) |
La distance focale de la lentille est
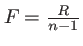 . Le nombre
. Le nombre
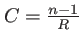 est appelé convergence ou vergence de la lentille. Celle-ci a ainsi pour effet de transformer une onde plane en onde sphérique.
est appelé convergence ou vergence de la lentille. Celle-ci a ainsi pour effet de transformer une onde plane en onde sphérique.
Le coefficient de transmission associé à une lentille divergente est obtenu en changeant simplement le signe - par un signe + dans l'équation 1.53. On obtient alors une onde sphérique divergente de focale négative
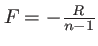 .
.
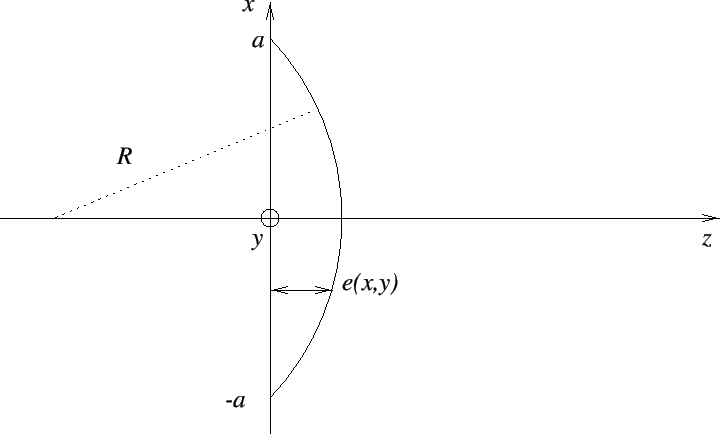
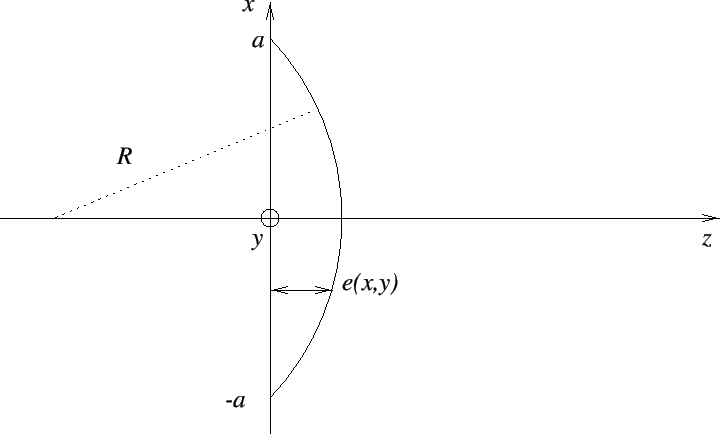
![]() appartenant à la surface bombée possède des coordonnées qui vérifient l'équation de la sphère. Le centre de la sphère se trouve en
appartenant à la surface bombée possède des coordonnées qui vérifient l'équation de la sphère. Le centre de la sphère se trouve en
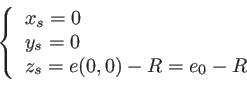
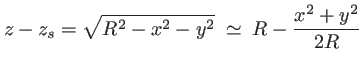
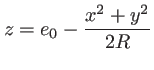
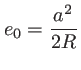
![$\displaystyle t(x,y)=e^{\frac{i\pi a^2 (n-1)}{\lambda R}}\; \exp\left[-\frac{i\pi (x^2+y^2)}{\lambda R} (n-1) \right]$](img363.png)
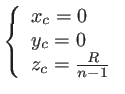
![]() .
.