Fente rectangulaire
Soit une fente rectangulaire de largeur 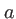 dans la direction
dans la direction 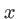 et
et 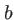 dans la direction
dans la direction 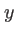 . Cette fente est éclairée sous incidence normale par une onde plane de longueur d'onde
. Cette fente est éclairée sous incidence normale par une onde plane de longueur d'onde 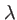 et d'amplitude
et d'amplitude 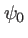 dans le plan de la fente. On note
dans le plan de la fente. On note 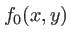 l'amplitude de l'onde à la sortie de la fente et
l'amplitude de l'onde à la sortie de la fente et 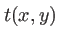 son coefficient de transmission. On a
son coefficient de transmission. On a
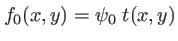 |
(1.56) |
avec
L'amplitude observée à une distance 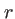 dans une direction
dans une direction
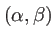 s'écrit :
s'écrit :
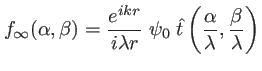 |
(1.57) |
avec
la définition du sinus cardinal est ici
sinc
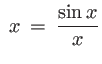
l'amplitude s'écrit alors
et l'intensité
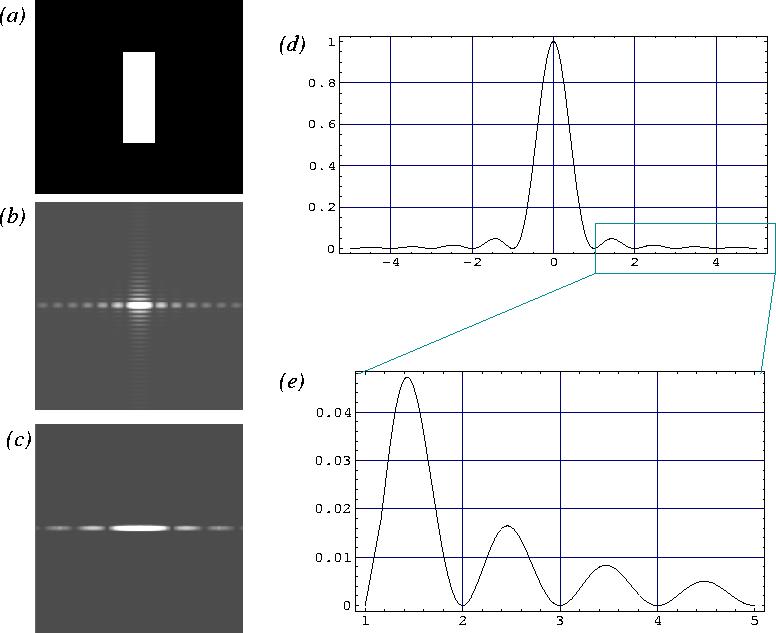
Cette fonction est représentée figure 1.12. Il est très facile de l'observer lorsqu'on dispose d'un petit laser en regardant sur un écran placé à quelques dizaines de centimètres de la fente. C'est une fonction qui est maximum en
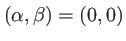 , qui présente un lobe principal entouré de pics secondaires situés en
, qui présente un lobe principal entouré de pics secondaires situés en
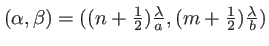 . Pour une fente beaucoup plus haute que large, l'aspect de l'intensité est celui d'une ligne pointillée.
. Pour une fente beaucoup plus haute que large, l'aspect de l'intensité est celui d'une ligne pointillée.
òÉÓ.:
Figure de diffraction d'une fente rectangulaire. L'intensité diffractée est décrite par une fonction sinus cardinal carré dans les deux sens (voir le texte). (a) Fente ; (b) Figure de diffraction (intensité) ; (c) Figure de diffraction d'une fente plus fine ; (d) Graphe de la fonction
sinc
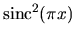 ; (e) Zoom de la courbe (d).
; (e) Zoom de la courbe (d).
|
Les positions et valeurs des maxima et minima secondaires dans la direction 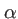 associée à la variable
associée à la variable 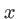 dans laquelle la taille de la fente est
dans laquelle la taille de la fente est 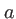 , sont donnés dans le tableau suivant :
, sont donnés dans le tableau suivant :
| |
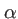
|
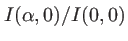
|
| 1er zéro |
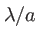
|
0 |
| 1er maximum secondaire |
1.5 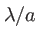
|
0.045 |
| 2e zéro |
2 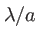
|
0 |
| 2e maximum secondaire |
2.5 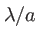
|
0.016 |
| 3e zéro |
3 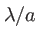
|
0 |
| 3e maximum secondaire |
3.5 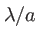
|
0.008 |
Il est donné par la première annulation du sinc. Pour une fente de largeur 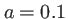 mm éclairée à la longueur d'onde
mm éclairée à la longueur d'onde 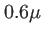 m, la taille
m, la taille
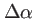 de ce lobe est
de ce lobe est
ce qui donne un angle de 0.7 degrés. On se trouve dans le cadre de l'optique paraxiale.
Le pourcentage d'intensité lumineuse contenue dans le pic principal est donné par le rapport des intégrales
le calcul numérique de ce rapport avec un ordinateur donne
le pic principal contient les 4/5 de l'énergie lumineuse. On assimilera souvent pour cette raison la taille de la figure de diffraction (en théorie infinie) à celle de son lobe principal.
Avec les valeurs numériques de notre exemple (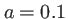 mm) l'approximation paraxiale est réalisée. On peut écrire la diffraction de Fresnel à l'aide la la transformée de Fourier-Fresnel. Le calcul fait intervenir des intégrales de Fresnel.
mm) l'approximation paraxiale est réalisée. On peut écrire la diffraction de Fresnel à l'aide la la transformée de Fourier-Fresnel. Le calcul fait intervenir des intégrales de Fresnel.
La figure 1.13 représente une simulation réalisée à l'aide d'un micro-ordinateur pour différentes valeurs de 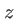 . Remarquer le passage progressif de la forme de la fente (éclairement dans le plan
. Remarquer le passage progressif de la forme de la fente (éclairement dans le plan 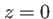 ) au sinus cardinal caractéristique de la diffraction à l'infini. L'approximation de Fraunhofer est ici possible,avec les valeurs
) au sinus cardinal caractéristique de la diffraction à l'infini. L'approximation de Fraunhofer est ici possible,avec les valeurs
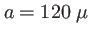 et
et
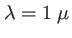 pour
pour
Fig. 1.13:
Figures de diffraction de Fesnel (intensité) d'une fente rectangulaire pour différentes distances entre le plan de la fente et le plan d'observation.

|
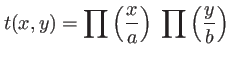
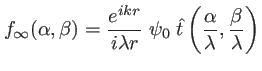
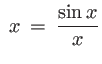
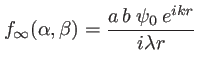 sinc
sinc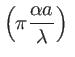 sinc
sinc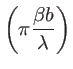
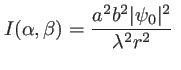 sinc
sinc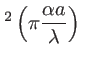 sinc
sinc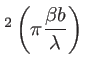

![]() associée à la variable
associée à la variable ![]() dans laquelle la taille de la fente est
dans laquelle la taille de la fente est ![]() , sont donnés dans le tableau suivant :
, sont donnés dans le tableau suivant :
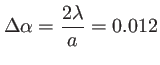
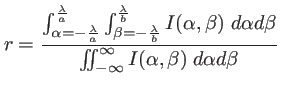
![]() . Remarquer le passage progressif de la forme de la fente (éclairement dans le plan
. Remarquer le passage progressif de la forme de la fente (éclairement dans le plan ![]() ) au sinus cardinal caractéristique de la diffraction à l'infini. L'approximation de Fraunhofer est ici possible,avec les valeurs
) au sinus cardinal caractéristique de la diffraction à l'infini. L'approximation de Fraunhofer est ici possible,avec les valeurs
![]() et
et
![]() pour
pour

