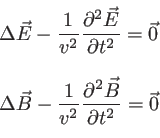 |
(1.1) |
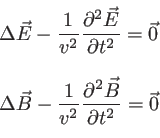 |
(1.1) |
L'onde plane est une solution particulière de cette équation. Les champs ne dépendent que d'une seule variable d'espace que l'on notera ici ![]() . L'équation de propagation se simplifie sous cette hypothèse et l'on montre que
. L'équation de propagation se simplifie sous cette hypothèse et l'on montre que ![]() et
et ![]() s'écrivent comme la somme de deux vibrations se propageant en sens inverse l'une de l'autre à la vitesse
s'écrivent comme la somme de deux vibrations se propageant en sens inverse l'une de l'autre à la vitesse ![]() :
:
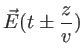 et
et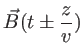
L'onde plane monochromatique ou onde plane sinusoïdale est une forme particulière de ces solutions pour lesquelles ![]() et
et ![]() sont des fonctions trigonométriques : cosinus, sinus ou plus généralement exponentielles complexes. Si
sont des fonctions trigonométriques : cosinus, sinus ou plus généralement exponentielles complexes. Si ![]() est la pulsation de la fonction trigonométrique on écrit :
est la pulsation de la fonction trigonométrique on écrit :
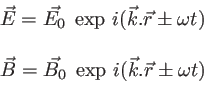 |
(1.2) |
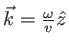 est le vecteur d'onde.
est le vecteur d'onde.
Généralement les ondes proviennent de sources quelque part dans l'espace et se propagent de la source vers le point courant (point où les champs sont calculés). On doit alors choisir le signe + ou - dans les expressions ci-dessus. Sauf indication contraire on choisira le signe - (propagation vers les ![]() , l'onde est dite progressive).
, l'onde est dite progressive).
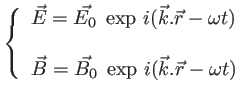 |
(1.3) |

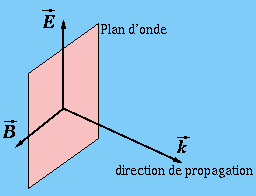
La structure de l'onde plane est schématisée par la figure ci-après. Les champs