Diffraction de Fresnel au foyer d'une lentille convergente

On éclaire une lentille mince convergente par une onde plane arrivant sous incidence normale. L'optique géométrique prévoit qu'une telle lentille focalise la lumière en un point au foyer. Nous allons retrouver ce résultat par la diffraction de Fresnel.

On se place dans l'aproximation de l'optique paraxiale, $z$ est l'axe de la propagation, la lentille est supposée de dimensions transversales infinies. On note

• $(x',y')$ les coordonnées dans le plan de la lentille $(z=0)$
• $(x,y)$ les coordonnées dans le plan d'observation
• $\psi_0$ l'amplitude
• $R$ et $n$ le rayon de courbure de la lentille et son indice de réfraction
• $f_z(x,y)$ l'amplitude dans le plan d'osbervation

Le coefficient de transmission de la lentille convergente s'écrit

$$t(x',y')=\exp -\frac{i\pi(n-1)(x'^2+y'^2)}{\lambda R}$$

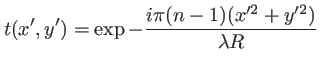
l'amplitude après la lentille s'écrit à l'aide de la transformée de Fourier-Fresnel. Il vient

$$f_z(x,y)=\psi_0 \; \frac{e^{ikz}}{i\lambda z} \; \exp \frac{i\pi ... ...}{\lambda z}} \left[ f_0(x',y') \exp\frac{i\pi}{\lambda z}(x'^2+y'^2) \right]$$

soit

$$f_z(x,y)=\psi_0 \; \frac{e^{ikz}}{i\lambda z} \; \exp \frac{i\pi ... ...i\pi}{\lambda}(x'^2+y'^2)\left(\frac{1}{z}-\frac{n-1}{R}\right) \right)\right]$$

Cette expression est particulièrement simple pour la valeur $z=\frac{R}{n-1}$ où l'exponentielle vaut 1. L'amplitude s'écrit alors :

$$f_z(x,y)=-i \psi_0 \lambda z e^{ikz} \; \delta(x,y)$$

Ce qui s'interprère comme un point de lumière extrèmement brillant sur l'axe optique : la lentille concentre toute la lumière incidente dans ce point qui apparait comme le foyer de la lentille. On retrouve ainsi la distance focale, inverse de la convergence

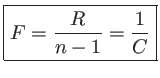$$\mbox{\fbox{$\displaystyle F=\frac{R}{n-1}=\frac{1}{C} $}}$$ (1.58)