Approximation paraxiale pour l'onde plane
On suppose que l'incidence de l'onde, c'est à dire l'angle formé par le vecteur d'onde et l'axe optique 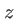 ,
est faible. C'est à dire
,
est faible. C'est à dire
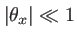 et
et
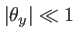 . C'est souvent le cas quand on fait des expériences optiques sur banc. Sous cette hypothèse, les cosinus directeurs s'écrivent sous la forme approchée suivante :
. C'est souvent le cas quand on fait des expériences optiques sur banc. Sous cette hypothèse, les cosinus directeurs s'écrivent sous la forme approchée suivante :
Chiffrons un ordre de grandeur de l'angle en dessous duquel on
peut considérer que l'on est en optique paraxiale. On approxime généralement 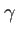 au
deuxième ordre pour des raisons qui seront vues plus loin. L'erreur que l'on fait sur
au
deuxième ordre pour des raisons qui seront vues plus loin. L'erreur que l'on fait sur 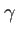 est égale au terme suivant du développement, soit
est égale au terme suivant du développement, soit
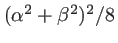 . Un angle de 1
. Un angle de 1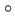 donne une erreur de l'ordre de 0.0001 sur
donne une erreur de l'ordre de 0.0001 sur 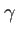 si l'on fait l'approximation paraxiale. Avec un angle de 10
si l'on fait l'approximation paraxiale. Avec un angle de 10 l'erreur sur
l'erreur sur 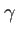 devient de l'ordre de 0.01. Au delà, l'erreur devient trop grande et l'approximation paraxiale devient trop imprécise.
devient de l'ordre de 0.01. Au delà, l'erreur devient trop grande et l'approximation paraxiale devient trop imprécise.
On retiendra que l'approximation paraxiale pour l'onde plane peut être faire si les angles d'inclinaison sont inférieurs à 10 .
.
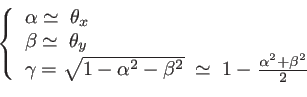
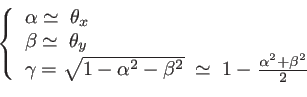
![]() .
.