Intensité d'une onde

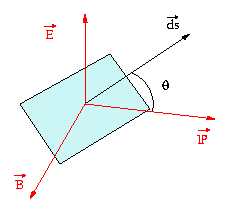
Ce qui donne, compte-tenu du fait que le champ électromagnétique doit être exrpimé en notation réelle pour faire le produit vectoriel :
d'où l'intensité instantannée de l'onde plane, définie positive,
Cette fonction sinusoïdale a une pulsation temporelle
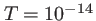 s environ dans le visible. L'oeil a un temps d'intégration de 40 ms environ, les caméras rapides ont des temps de pose de l'ordre de la milliseconde et ne voient en fait pas cette fonction
s environ dans le visible. L'oeil a un temps d'intégration de 40 ms environ, les caméras rapides ont des temps de pose de l'ordre de la milliseconde et ne voient en fait pas cette fonction
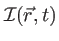 mais sa moyenne sur le temps de pose
mais sa moyenne sur le temps de pose 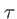 , soit la quantité
, soit la quantité 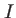 :
:
Pour l'oeil, l'intégrale porte sur plus de 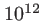 périodes du
périodes du 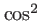 , et pour les caméras rapides on intègre environ
, et pour les caméras rapides on intègre environ 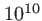 périodes. L'intégrale vaut alors
périodes. L'intégrale vaut alors
et la valeur moyenne d'un 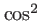 étant de 1/2, l'intensité est donnée par
étant de 1/2, l'intensité est donnée par
On obtient ainsi le résultat suivant lequel, pour une onde plane monochromatique, l'intensité est proportionnelle au module du champ électrique de l'onde
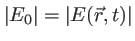 . Par habitude, on pose la constante de proportionalité égale à 1. On écrira
. Par habitude, on pose la constante de proportionalité égale à 1. On écrira
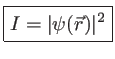 |
(1.9) |
avec
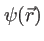 l'attention est attirée sur le fait que la quantité
l'attention est attirée sur le fait que la quantité 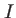 n'est ici plus homogène à une puissance par unité de surface (W/m
n'est ici plus homogène à une puissance par unité de surface (W/m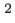 ), mais au carré d'un champ électrique.
), mais au carré d'un champ électrique.
Le calcul d'intensité, établi dans le cas d'une onde plane (dont les surfaces d'onde sont des plans) se généralise aux ondes monochromatiques d'amplitude complexe
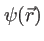 quelconque, s'écrivant
quelconque, s'écrivant
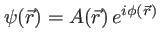 avec
avec 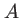 et
et 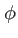 réels. Les surfaces d'ondes sont en effet assimilables localement à des plans sur la surface
réels. Les surfaces d'ondes sont en effet assimilables localement à des plans sur la surface 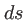 définie au paragraphe précédent autour du point
définie au paragraphe précédent autour du point 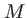 . Un développement limité permet de s'en convaincre, en effet :
. Un développement limité permet de s'en convaincre, en effet :
avec 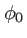 une constante, et
une constante, et
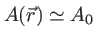 avec
avec 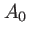 une constante (on ne gardera que l'ordre 0 qui suffit pour le terme
une constante (on ne gardera que l'ordre 0 qui suffit pour le terme 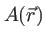 ). Ainsi l'amplitude complexe de l'onde s'approxime, autour du point
). Ainsi l'amplitude complexe de l'onde s'approxime, autour du point 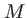 , par
, par
c'est à dire une onde plane, avec
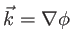 un vecteur d'onde ``local'', gradient de la phase de l'onde au point
un vecteur d'onde ``local'', gradient de la phase de l'onde au point 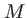 . Le raisonnement qui a conduit au calcul de l'intensité pour une onde plane s'applique donc aussi au cas d'une onde quelconque qui est localement plane. L'intensité est donc là aussi le carré du module de l'amplitude complexe
. Le raisonnement qui a conduit au calcul de l'intensité pour une onde plane s'applique donc aussi au cas d'une onde quelconque qui est localement plane. L'intensité est donc là aussi le carré du module de l'amplitude complexe
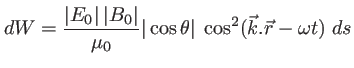


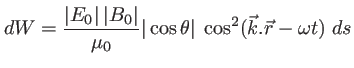
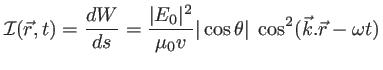
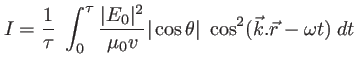
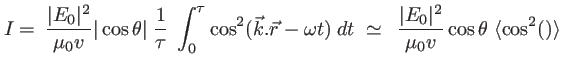
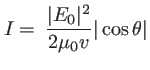
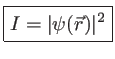
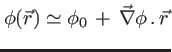
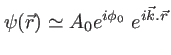
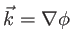 un vecteur d'onde ``local'', gradient de la phase de l'onde au point
un vecteur d'onde ``local'', gradient de la phase de l'onde au point