Une one plane monochromatique
d'amplitude complexe 
(on n'écrira pas la dépendance temporelle, le
système étant supposé stationnaire) éclaire sous incidence normale un écran percé de deux trous identiques de diamètre a
et distants de D. Ces trous sont placés le long de l'axe x centrés
sur les points de coordonnées 
et 
. Le
coefficient de transmission 
de l'écran peut alors s'écrire, si t
désigne celui d'un seul trou :
L'amplitude diffractée dans une direction 
s'écrit à
partir de la transformée de Fourier bidimensionnelle de l'amplitude de l'onde
à la sortie de l'écran. On peut aisément calculer cette transformée de Fourier
en s'aidant de la propriété suivante :
on en déduit
avec
L'intensité diffractée 
s'écrit (I désignant la fonction d'Airy) :
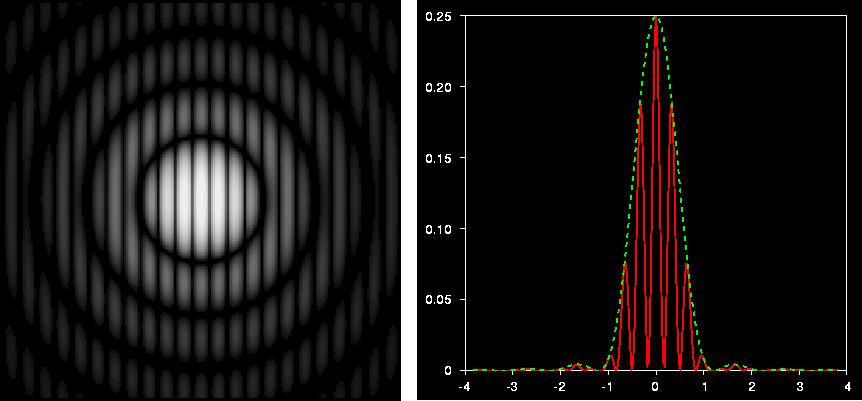
on remarque que la figure de diffraction n'est pas à symétrie de révolution
comme dans le cas d'un sel trou. Il s'agit d'une fonction
d'Airy striée de franges perpendiculaires à la direction des trous. La figure
ci-dessous représente la fonction en niveaux de gris et une
coupe le long de l'axe 
.
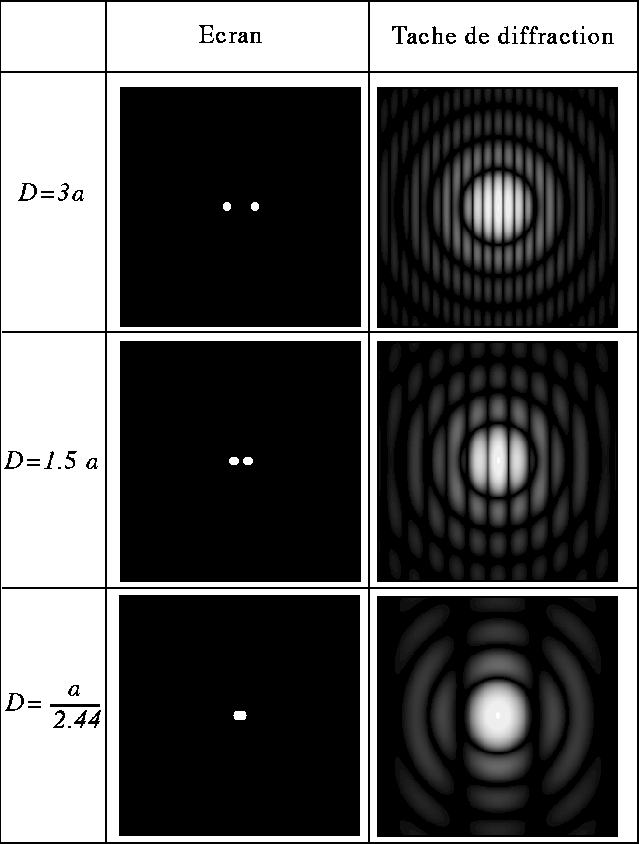
Le nombre de franges à l'intérieur de la tache centrale est donné par le diamètre du premier anneau noir
divisé par l'interfrange ; il vaut 2.44 D/a. Si D augmente, les franges se
resserrent, si D diminue, les franges s'écartent. Lorsque D devient inférieur
à 
, l'interfrange devient plus grand que le premier
anneau noir et les franges disparaissent. Le comportement de la figure de
diffraction en fonction de D est illustré dans le tableau ci-dessous.
Un cas particulier intéressant est celui où la dimension des trous devient très
petite ( 
). La fonction d'Airy devient alors constante et la figure
de diffraction tend vers une fonction cosinus carré : on
retrouve l'intensité produite par l'expérience des trous d'Young.
La figure de diffraction de deux trous peut s'observer avec un télescope si on pose devant l'ouverture un cache percé de deux trous (2 ou 3 centimètres de diamètre suffisent). En pointant une étoile brillante et en forçant le grossissement, on voit apparaitre la tache d'Airy des petits trous, striée de franges d'autant plus fines que les trous sont écartés. J'ai fait ça au télescope de 60 centimètres du Pic du Midi, c'était superbe. On a vu de magnifiques franges sur Capella en mettant un filtre vert pour se rapprocher de la condition "monochromatique"...
On suppose dans ce paragraphe que l'un des deux trous (ils sont toujours
circulaires et de diamètre a) laisse passer moins de lumière que l'autre,
comme si on lui avait mis un filtre. Soit 
la transmission de ce trou
( 
). Dans ce cas le coefficient de transmission de l'écran
s'écrit
l'intensité résultante de la figure de diffraction devient (I désigne toujours la fonction d'Airy)
Une coupe de cette fonction est représentée ci-dessous pour deux valeurs de
.
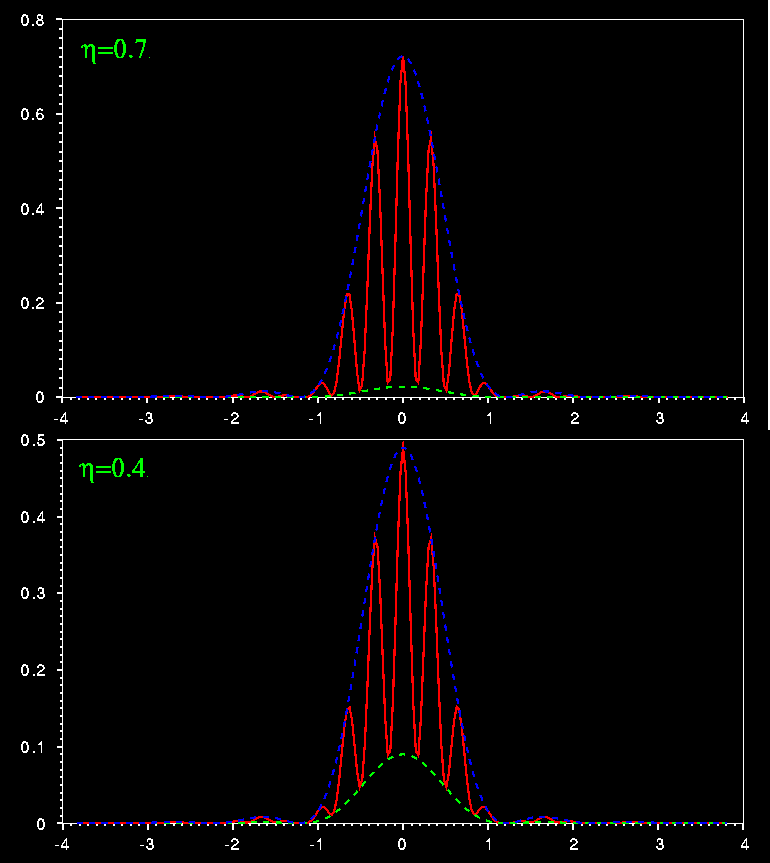
On remarque que les franges sont cette fois affectées d'un contraste (le minimum
de lumière ne correspond pas à une intensité nulle), qui varie en fonction de
. Les franges sont en fait enveloppées entre les deux fonctions
et 
dessinées en
pointillés sur le graphe ci-dessus.