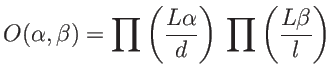
Degré de cohérence spatiale : par définition
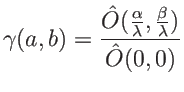 avec ici
avec ici 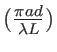
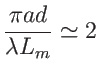 (la table de sinc donne sinc(2)=0.45). Ce qui donne
(la table de sinc donne sinc(2)=0.45). Ce qui donne
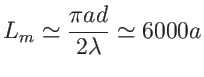
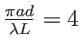 et le contraste vaut
et le contraste vaut
28 Avril 2015
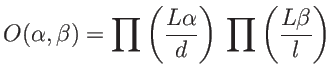
Degré de cohérence spatiale : par définition
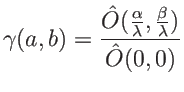 avec ici
avec ici 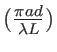
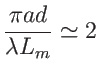 (la table de sinc donne sinc(2)=0.45). Ce qui donne
(la table de sinc donne sinc(2)=0.45). Ce qui donne
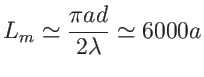
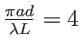 et le contraste vaut
et le contraste vaut
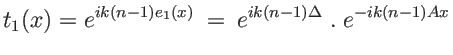
avec
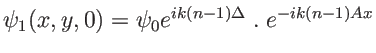 . Il s'agit d'une onde plane, comme prévu. Pour l'écrire en
. Il s'agit d'une onde plane, comme prévu. Pour l'écrire en
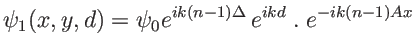
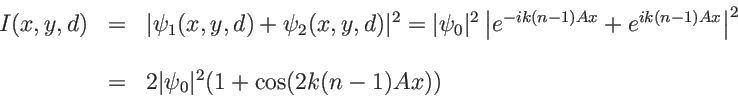
Ce sont des franges de constraste 1 et d'interfrange
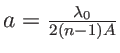
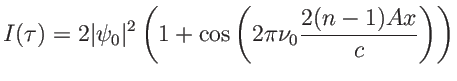
CQFD avec
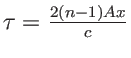 . La variable
. La variable
avec
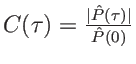 et
et
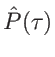 .
.
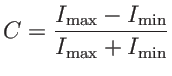
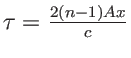 permet d'écrire
permet d'écrire
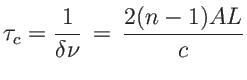
A.N. :
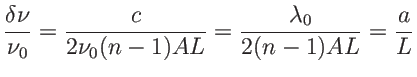 avec
avec 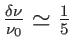 .
.
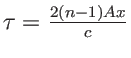 . Il vient
. Il vient
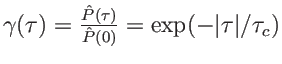 . On a donc
. On a donc
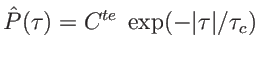 . Le formulaire de TF permet de calculer la TF inverse. Il vient
. Le formulaire de TF permet de calculer la TF inverse. Il vient
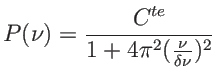
Et le spectre
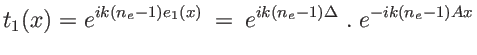
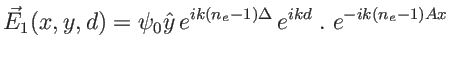
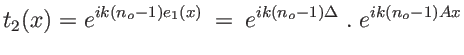
et le champ dans le plan
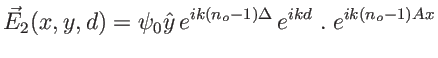
![$\displaystyle I=\vert E_1(x,y,d)+E_2(x,y,d)\vert^2=2 \vert\psi_0\vert^2\: \left[1+\cos(k(n_e-n_o)\Delta-k(n_e+n_o-2) Ax ) \right]
$](img76.png)
L'interfrange est
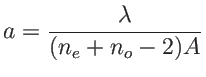 , l'origine des franges est en
, l'origine des franges est en
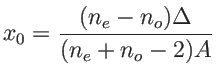 . Lorsque les deux indices sont égaux, on retrouve les résultats de la question 3.
. Lorsque les deux indices sont égaux, on retrouve les résultats de la question 3.
![$\displaystyle I'=2 \vert\psi_0\vert^2\: \left[1+\cos(k(n_o-n_e)\Delta-k(n_e+n_o-2) Ax ) \right]
$](img81.png)
le seul changement est sur la position de la frange centrale (
Vecteur de Jones du champ incident dans la base des lignes neutres
![]() :
:
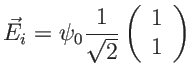
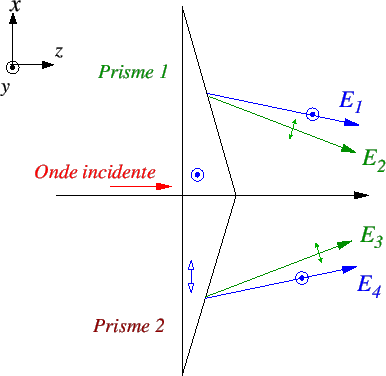
La composante ![]() du champ incident donne naissance (comme à la question 7) à deux ondes
du champ incident donne naissance (comme à la question 7) à deux ondes ![]() et
et ![]() (voir schéma ci-dessous),polarisées selon
(voir schéma ci-dessous),polarisées selon ![]() . Les amplitudes valent
. Les amplitudes valent
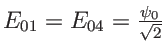 . Les vecteurs d'onde ont été calculés en question 7c et 7d. On a
. Les vecteurs d'onde ont été calculés en question 7c et 7d. On a
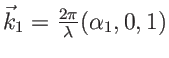 et
et
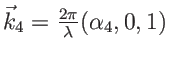 avec
avec
![]() et
et
![]() .
.
La composante ![]() du champ incident donne naissance (comme à la question 8) à deux ondes
du champ incident donne naissance (comme à la question 8) à deux ondes ![]() et
et ![]() , de polarisation rectiligne presque parallèle à
, de polarisation rectiligne presque parallèle à ![]() . Les amplitudes valent
. Les amplitudes valent
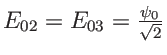 . Les vecteurs d'onde sont
. Les vecteurs d'onde sont
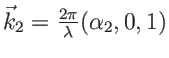 et
et
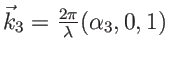 avec
avec
![]() et
et
![]()