Correction du second partiel d'optique
Année 2009-2010
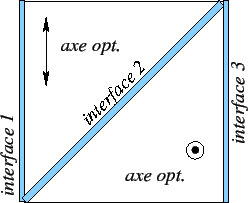
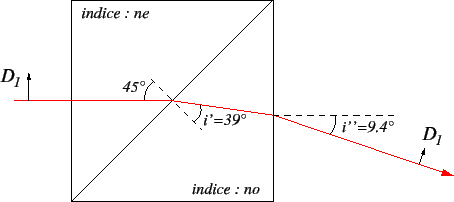
Le prisme possède 3 interfaces, numérotées 1, 2 et 3 dans le schéma ci-dessous.
- Une onde est non polarisée quand son champ électrique a une
orientation aléatoire dans le plan d'onde au cours du temps (toutes les
orientations sont équiprobables).
- Un matériau uniaxe est un matériau pour lequel il existe un axe
pivilégié appelé axe optique. Un champ électrique polarisé suivant
l'axe optique se propage avec une vitesse
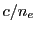 (
(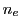 est appéle indice extraordinaire). Un champ électrique polarisé dans le
plan perpendiculaire à l'axe optique se propage avec une vitesse
est appéle indice extraordinaire). Un champ électrique polarisé dans le
plan perpendiculaire à l'axe optique se propage avec une vitesse 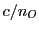 (
(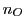 est l'indice ordinaire)
est l'indice ordinaire)
- Pour un milieu non chargé éclairé par une onde plane sinusoïdale, la première équation de Maxwell (
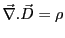 ) conduit à
) conduit à
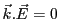 avec
avec 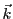 le vecteur d'onde. Le champ électrique est donc dans le plan perpendiculaire à
le vecteur d'onde. Le champ électrique est donc dans le plan perpendiculaire à 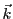 et n'a que deux composantes non nulles (ici selon
et n'a que deux composantes non nulles (ici selon 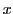 et
et 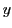 )..
)..
-
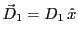 est l'onde extraordinaire dans le premier prisme (axe optique
est l'onde extraordinaire dans le premier prisme (axe optique
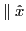 ).
).
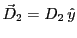 est l'autre composante (ordinaire dans le premier prisme).
est l'autre composante (ordinaire dans le premier prisme).
- L'onde correspondant à la polarisation
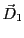 est déviée aux interfaces 2 et 3. Dans le prisme 1 l'indice est
est déviée aux interfaces 2 et 3. Dans le prisme 1 l'indice est 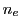 , dans le prisme 2 l'indice est
, dans le prisme 2 l'indice est 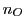 . La déviation à l'interface 2 se calcule à l'aide de la loi de Descartes
. La déviation à l'interface 2 se calcule à l'aide de la loi de Descartes
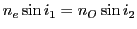 . Le trajet est le suivant :
l'angle d'émergence est noté
. Le trajet est le suivant :
l'angle d'émergence est noté 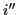 . Le vecteur d'onde dans le prisme 1 est
. Le vecteur d'onde dans le prisme 1 est
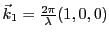 . Dans le prisme 2 il vaut
. Dans le prisme 2 il vaut
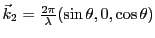 avec
avec
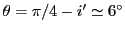 . Dans le vide à la sortie il vaut
. Dans le vide à la sortie il vaut
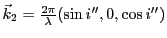
- Pour l'onde correspondant à la polarisation
 . L'indice est cette fois
. L'indice est cette fois 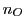 dans le prisme 1 et
dans le prisme 1 et 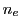 dans le prisme 2. Le trajet est le suivant :
dans le prisme 2. Le trajet est le suivant :
- Pour le prisme 1 l'angle d'émergence vaut
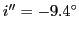 . Pour le prisme 2 il vaut
. Pour le prisme 2 il vaut
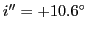 .
.
- On n'a qu'un seul rayon réfracté par la face 2 quand
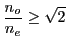 . Dans ce cas l'onde correspondant à la polarisation
. Dans ce cas l'onde correspondant à la polarisation 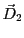 subit une réflextion totale (l'application de la loi de Descartes conduit à
subit une réflextion totale (l'application de la loi de Descartes conduit à
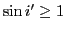 ). Seule la polarisation
). Seule la polarisation 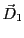 est alors transmise : l'onde émergente est polarisée linéairement, comme à la sortie d'un polariseur.
est alors transmise : l'onde émergente est polarisée linéairement, comme à la sortie d'un polariseur.
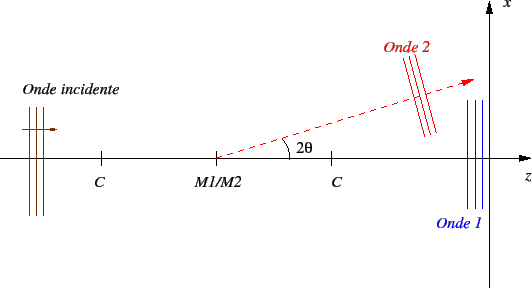
- Schéma équivalent plus simple. La déviation de l'onde 2 est
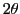 .
.
- Onde monochromatique
- La longueur de cohérence d'une onde est la distance maximale entre
deux fronts d'onde cohérents. Elle est infinie pour une onde
monochromatique.
- En utilisant l'approximation paraxiale, on a
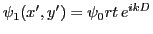 et
et
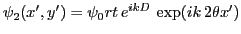
-
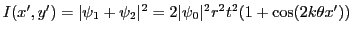 . On observe des franges rectilignes parallèles à
. On observe des franges rectilignes parallèles à 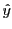 .
.
- Interfrange
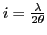 contraste 1
contraste 1
- Différence de marche :
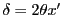 (on peut le voir soit géométriquement soit par l'identification au déphasage entre
(on peut le voir soit géométriquement soit par l'identification au déphasage entre 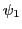 et
et 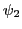 :
:
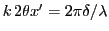 ).
).
- Retard
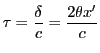 . Intensité en fonction de
. Intensité en fonction de 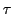 :
:
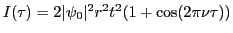 en posant
en posant
 .
.
- Onde quasi-monochromatique
- Le spectre
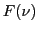 d'une onde représente l'intensité émise dans la bande de fréquence
d'une onde représente l'intensité émise dans la bande de fréquence
![$ [\nu,\nu+d\nu]$](img44.png)
- Ici
 est centrée sur
est centrée sur  . Elle s'écrit
. Elle s'écrit
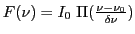 .
.
- Longueur de cohérence
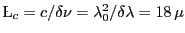 m
m
- Degré complexe de cohérence
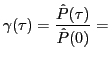
sinc
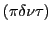
- Intensité en fonction
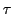 : elle se déduit de celle de la question 2f, en remplaçant le terme
: elle se déduit de celle de la question 2f, en remplaçant le terme
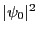 par
par 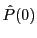 . Il vient
. Il vient
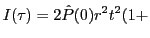
sinc
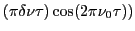
- Fonction contraste
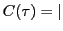 sinc
sinc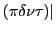
- Intensité en fonction de
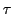
![\includegraphics[width=20cm]{int_raielarge.eps}](img63.png)
-
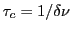 (premier zéro positif du sinc)
(premier zéro positif du sinc)
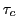 est le temps de cohérence
est le temps de cohérence
- Nombre de franges = rapport de la largeur du paquet central à l'interfrange
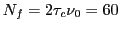 .
.
- Interfrange
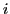 en mètres : on réécrit l'intensité en utilisant le changement de variable
en mètres : on réécrit l'intensité en utilisant le changement de variable
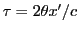 . Il vient
. Il vient
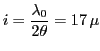 m
m
- Taille du paquet central de franges
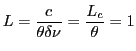 mm.
mm.



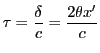 . Intensité en fonction de
. Intensité en fonction de 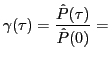 sinc
sinc![\includegraphics[width=20cm]{int_raielarge.eps}](img63.png)
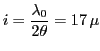 m
m
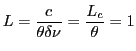 mm.
mm.