L2 - Partiel numéro 1

1993 - 1994

1. Question de Cours (au choix)

Réponse en 10 lignes

Signaux (quasi)périodiques et chaotiques

1. Quelles différences y-a-t'il, au niveau de la fonction d'autocorrélation et au niveau de la répartition spectrale de puissance, entre un signal quasi-périodique et un signal chaotique ?
2.  Quelles sont les causes d'élargissement des raies lumineuses ? Donner l'allure des fonctions d'autocorrélation.

 

Echantillonnage : théorème de Shannon

1. Qu'est-ce qu'une fonction échantillonnée ? Quelle est la relation liant la TF d'une fonction et de son échantillonée ? (on de demande pas de démonstration)
2. Expliquer pourquoi et comment (en principe) on peut déduire une fonction de son échantillonnée si son spectre contient des fréquences 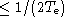 (  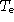est la période déchantillonnage).

 

Interférences et cohérence temporelle

1. On considère une raie lumineuse dont la répartition spectrale est 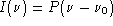 . Montrer que le caractère non parfaitement monochromatique introduit un contraste supplémentaire




2. A quelle conition sur 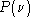 ,  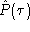est-il réel ?

2. Exercice : Filtrage en lumière cohérente

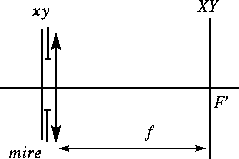
On considère une mire de coefficient de transmission (en amplitude)

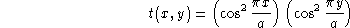
limitée par un diaphragme circulaire de rayon 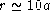 et éclairée sous incidence normale par une onde plane de longueur d'onde  .

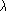1. Décrire la figure de diffraction de Fraunhofer dans le plan F'XY. A.N. : 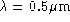 ,  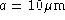, f=1 m.
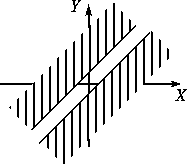
2.  Dans le plan X,Y on place une fente à 45  de largeur 1 cm. Décrire l'objet filtré. Commentaires ?

3. Exercice : Onde sphérique et Principe de Huygens-Fresnel

Dans le plan z=0 on considère une onde d'amplitude

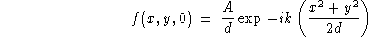
se propageant vers les z>0, la dépendance en temps étant  .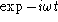

1. S'agit-il d'une onde convergente ou d'une onde divergente ?
2.  A l'aide de la formule d'Huygens-Fresnel




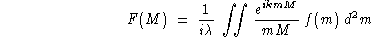
et de



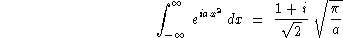
calculer f(0,0,z) (z>0) pour un point M sur l'axe. Commentaires ?

4. Problème : Filtrage en lumière incohérente

On considère un objet éclairé en lumière spatialement incohérente de longueur d'onde 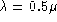 m, caractérisé par une répartition d'intensité périodique :

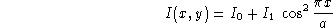
et qui est situé à la distance D de la pupille d'entrée d'un appareil photo (on supposera 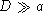 et la mise au point de l'appareil photo réglée sur l'infini).

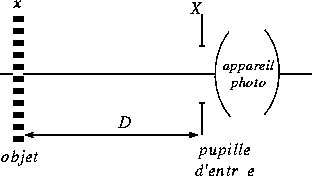
Soit P(X) le coefficient de transmission en amplitude de la pupille (indépendant de Y) ; on rappelle que la fonction de transfert de l'appareil est proportionnelle à :

1. Qu'est-ce qu'un objet spatialement incohérent ?
2.  Quel est le contraste de cet objet ? (A.N:  ).
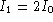3.  Qu'est-ce que la pupille d'entrée d'un instrument ?
4.  Qu'est-ce que la fonction de transfert d'un instrument ?
5.  Quelles sont les fréquences angulaires présentes dans l'objet ? A.N. : a=0.5 cm, D=5 m.
1. La pupille d'entrée est une fente de largeur l=1 mm.
1. Dessiner le graphe de la fonction 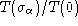 . (On pourra admettre que T est une fonction triangle).
2.  Déterminer l'objet filtré. En quoi diffère-t-il de l'objet ?
2. Pour décrire un effet de défocalisation de l'appareil photo, on suppose que 
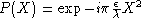
1. Montrer que celà revient à mettre dans le plan XY une lentille cylindrique dont on précisera la convergence C (la lentille est prise cylindrique pour éviter une dépendance en Y).
2.  Montrer que si on considère la pupille comme ``infinie'', 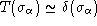 . Interprétation ? Si la pupille est centrée et de largeur  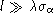, montrer que :




La largeur de la pupille étant fixée à l=1 cm, on défocalise l'appareil progressivement (en augmentant  à partir de  ).

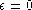3. Quand l'intensité de l'objet filtré devient-elle uniforme pour la première fois ? A.N. : a=0.5 cm, D=5 m.
4. Expliquer pourquoi, quand on continue à défocaliser, on obtient un objet filtré qui est à nouveau périodique mais dont les maxima d'intensité sont situés à la place des minima d'intensité de l'objet, puis un objet filtré uniforme, puis...etc.