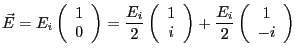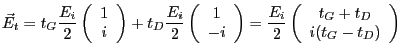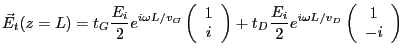L3 Physique -- Correction de l'examen d'optique
2e session - Janvier 2010
Date: (barême sur 25 points : 13 pour l'exercice 1 et 12 pour le 2)
- L'onde est sphérique dans la région
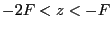
- La source est en
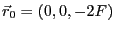 . L'amplitude complexe de l'onde en
. L'amplitude complexe de l'onde en
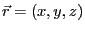 s'écrit
s'écrit
- Dans l'approximation paraxiale, en posant
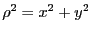 :
:
- Dans l'approximation paraxiale on fait l'hypothèse que les rayons
sont peu inclinés sur l'axe optique. Ici celà revient à supposer que
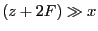 et
et 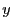 .
.
- On fait
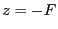 dans l'expression de
dans l'expression de 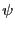 . Il vient
. Il vient
- Coefficient de transmission de la lentille
- Amplitude complexe de l'onde en
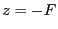 juste après la lentille
juste après la lentille
- Cette onde est plane et se propage dans la direction
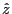
- Amplitude complexe en
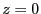 juste avant la traversée du réseau : il suffit de propager l'onde plane sur une distance
juste avant la traversée du réseau : il suffit de propager l'onde plane sur une distance 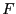
- On écrit d'abord le coefficient de transmission du réseau
l'amplitude complexe à la sortie du réseau est
l'amplitude diffractée à l'infini est donc
et l'intensité correspondante
- Une onde plane éclairant un réseau donne naissance en sortie à un
ensemble d'ondes planes que l'on appelle les ordres. On le voit dans
l'expression de l'intensité : présence de pics (le sha) correspondant
chacun à une figure de diffraction d'onde plane
- L'ordre
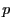 se trouve ici dans la direction
se trouve ici dans la direction
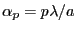 (période du
(période du
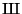 ) et
) et 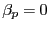 (présence de
(présence de
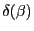 .
.
- Reprendre les questions 2,3,5,7,9,10,12 dans le cas où la source est déplacée au point
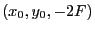
- question 2 :
- question 3 :
- question 5 :
- question 7 :
c'est une onde plane inclinée de la forme
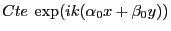 avec
avec
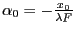 et
et
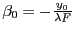
- question 9 : pour écrire cette onde dans le plan
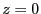 , il suffit de la multiplier par
, il suffit de la multiplier par
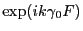 avec
avec
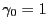 en optique paraxiale. Il vient
en optique paraxiale. Il vient
- question 10 :
L'amplitude diffractée à l'infini s'écrit maintenant
- question 12 : la direction de l'ordre
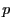 est donnée par les ``dents'' du peigne de Dirac ci-dessus. Il vient
est donnée par les ``dents'' du peigne de Dirac ci-dessus. Il vient
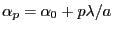 et
et
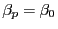 .
.
- Au foyer d'une lentille convergente on observe la figure de
diffraction (de Fraunhöffer) de l'amplitude complexe incidente. On a
ici deux lentilles convergentes d'où le nom de montage à double
diffraction.
- L'amplitude complexe dans le plan
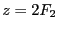 se déduit de celle qu'on observe dans le plan
se déduit de celle qu'on observe dans le plan 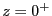
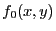 (voir question 10 ci-dessus) par une TF optique ; il vient :
(voir question 10 ci-dessus) par une TF optique ; il vient :
d'où
- L'ordre
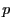 se trouve en
se trouve en
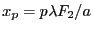 ,
, 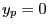
- On limite le réseau par un diaphragme circulaire de diamètre
 .
.
- Le nouveau coefficient de transmission du réseau est
- Amplitude complexe dans le plan
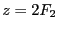 : elle fait apparaitre une convolution par un
: elle fait apparaitre une convolution par un 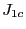 . Le calcul donne, en écrivant le sha comme une somme de distributions
. Le calcul donne, en écrivant le sha comme une somme de distributions 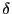
Il s'agit d'une somme de fonctions 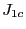 de largeurs voisines de
de largeurs voisines de
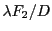 centrées en
centrées en
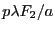
- Si
 , il n'y a pas de recouvrement entre les
, il n'y a pas de recouvrement entre les 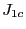 de la somme ci-dessus. Les termes de type ``double produit'' s'éliminent dans le calcul de l'intensité. Il vient
de la somme ci-dessus. Les termes de type ``double produit'' s'éliminent dans le calcul de l'intensité. Il vient
- La largeur de chaque tache correspondant est
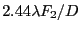 si l'on prend comme définition de la largeur le diamètre du premier anneau noir de la fonction d'Airy
si l'on prend comme définition de la largeur le diamètre du premier anneau noir de la fonction d'Airy 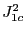 .
.
- Le pouvoir de résolution du réseau est sa capacité à séparer les images à deux longueurs d'ondes en deux taches distinctes.
Il vaut
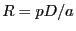 dans l'ordre
dans l'ordre 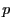
- L'intensité est la somme des intensités correspondant à chaque longueur d'ondes
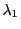 et
et  . En utilisant le résultat de la question 2, il vient
. En utilisant le résultat de la question 2, il vient
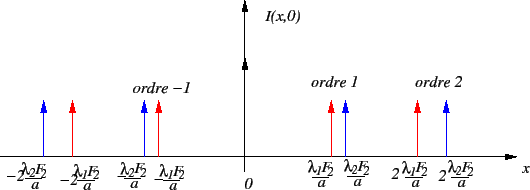
- Graphe de l'intensité
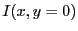 .
.
- Le premier peigne possède des maxima d'intensité en
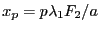 , le second en
, le second en
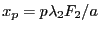 . Chaque ordre
. Chaque ordre 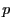 est ainsi dédoublé en deux pics séparés de
est ainsi dédoublé en deux pics séparés de
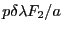 . sauf l'ordre 0 qui reste unique (en revanche il est deux fois plus lumineux).
. sauf l'ordre 0 qui reste unique (en revanche il est deux fois plus lumineux).
- On limite à nouveau le réseau par le diaphragme circulaire de diamètre
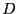 .
.
- Intensité dans le plan
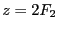 : c'est la somme des intensités correspondant à chaque longueur d'onde (question 4c). Il vient :
: c'est la somme des intensités correspondant à chaque longueur d'onde (question 4c). Il vient :
- Chaque ordre
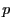 est ainsi constitué de la somme de deux fonctions d'Airy, sauf l'ordre 0
est ainsi constitué de la somme de deux fonctions d'Airy, sauf l'ordre 0
- Les taches correspondant à chaque ordre sont centrées en
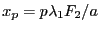 , le second en
, le second en
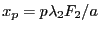 . Elles sont de largeur
. Elles sont de largeur
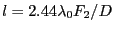 (en utilisant l'hypothèse
(en utilisant l'hypothèse
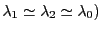 .
On a superposition des taches si leur séparation est inférieure à leur
demi-largeur (voir cours sur les réseaux), c'est à dire si
.
On a superposition des taches si leur séparation est inférieure à leur
demi-largeur (voir cours sur les réseaux), c'est à dire si
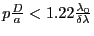 .
.
- Le critère de Rayleigh correspond à la situation ou les deux longueurs d'onde sont juste séparées dans l'ordre
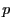 , c'est à dire
, c'est à dire
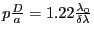
- Si les deux longueurs d'onde sont juste séparées dans l'ordre
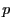 , elles seront confondues dans l'ordre
, elles seront confondues dans l'ordre 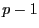 (leur séparation est plus faible dans l'ordre
(leur séparation est plus faible dans l'ordre 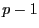 ) et très séparées dans l'ordre
) et très séparées dans l'ordre 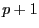 .
.
- Ce milieu est-il anisotrope à cause de
![$ [\sigma]$](img75.png) . Ainsi si le champ électrique est dirigé suivant
. Ainsi si le champ électrique est dirigé suivant 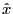 la conductivité n'a pas même valeur que s'il est dirigé suivant
la conductivité n'a pas même valeur que s'il est dirigé suivant 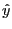
-
- Equations de Maxwell dans ce milieu (écrites ici en fonction des champs
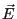 et
et 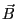 ) :
) :
- Si
 alors
alors
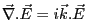 ,
,
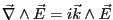 et
et
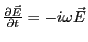
- La 3e équation de Maxwell donne
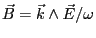 . Dans la quatrième, le terme
. Dans la quatrième, le terme
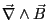 s'écrit alors
s'écrit alors
![$ i\vec k \wedge \vec B=i\vec k \wedge (\vec k \wedge \vec E)/\omega=i[ \vec k (\vec k.\vec E)-\vec E (\vec k.\vec k)]/\omega$](img96.png) . En injectant cette forme dans la 4e équation de Maxwell et en utilisant l'identité
. En injectant cette forme dans la 4e équation de Maxwell et en utilisant l'identité
 on obtient la relation demandée.
on obtient la relation demandée.
- En projetant la relation (1) sur l'axe
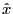 , et compte-tenu que
, et compte-tenu que
 on obtient
on obtient
De même la projection sur 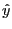 donne
donne
- En combinant les 2 équations ci-dessus pour éliminer le champ électrique, on obtient
qui donne deux solutions (une avec le signe +, l'autre avec le signe -). Il vient
- Dans un diélectrique la relation
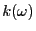 s'écrit
s'écrit
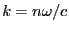 où
où 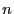 est l'indice du milieu. Si
est l'indice du milieu. Si 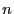 dépend de
dépend de 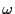 ,
la vitesse de la lumière dans le milieu dépend de la fréquence. Une
onde polychromatique sera dispersée en ses différentes couleurs après
traversée du milieu (certaines fréquences traversent plus vite que
d'autres). D'uù le nom de relation de dispersion.
,
la vitesse de la lumière dans le milieu dépend de la fréquence. Une
onde polychromatique sera dispersée en ses différentes couleurs après
traversée du milieu (certaines fréquences traversent plus vite que
d'autres). D'uù le nom de relation de dispersion.
- Pour une polarisation linéaire le vecteur de Jones peut s'écrire
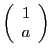 avec
avec 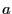 réel. Pour une circulaire c'est
réel. Pour une circulaire c'est
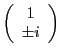 (déphasage de
(déphasage de 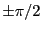 entre les composantes) du champ électrique).
entre les composantes) du champ électrique).
- En injectant la relation de dispersion (question 7) dans les relations de la question 6 on obtient
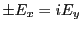 , c'est à dire
, c'est à dire
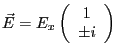 qui correspond à une polarisation circulaire (gauche ou droite). Ce sont donc ces ondes qui se propagent dans le milieu.
qui correspond à une polarisation circulaire (gauche ou droite). Ce sont donc ces ondes qui se propagent dans le milieu.
- La relation de dispersion conduit à
Dans le cas où
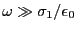 et compte-tenu de l'hypothèse
et compte-tenu de l'hypothèse
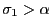 , la quantité
, la quantité
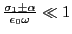 et un développement limité est possible. Il vient
et un développement limité est possible. Il vient
qui donne deux valeurs possibles pour l'indice :
![$ \displaystyle n=\left[1+\frac{\sigma_1\pm\alpha}{2\epsilon_0\omega} \right]$](img118.png) .
Un des indices est celui de la vibration circulaire gauche, l'autre est
celui de la circulaire droite. Les vitesses de phase des ondes
s'obtiennent par
.
Un des indices est celui de la vibration circulaire gauche, l'autre est
celui de la circulaire droite. Les vitesses de phase des ondes
s'obtiennent par
![$ \displaystyle v=c/n\simeq c\left[1-\frac{\sigma_1\pm\alpha}{2\epsilon_0\omega} \right]$](img119.png)
- En
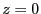 le champ électrique s'écrit
le champ électrique s'écrit
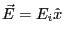 .
.
-
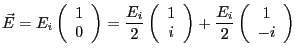
- En
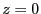 le champ transmis est
le champ transmis est
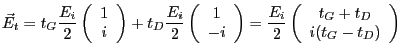
- La polarisation de l'onde transmise en
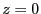 est elliptique
est elliptique
- Ecrire le champ transmis en
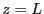 s'écrit
s'écrit
avec 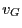 et
et 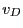 les vitesses de phase des ondes polarisées circulaire gauche et droite.
les vitesses de phase des ondes polarisées circulaire gauche et droite.
- Un milieu optiquement actif fait tourner la direction de polarisation de la lumière vers la gauche ou la droite.
- C'est le cas ici parce que les vitesses de propagation des
polarisations circulaires droite et gauche sont différentes. Une
vibration incidente de polarisation linéaire se transforme en
elliptique, l'axe principal de l'ellipse tourne au fur et à mesure que
l'épaisseur traversée augmente. Le calcul a été fait en TD.
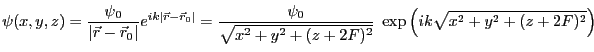
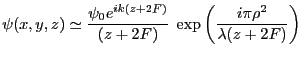
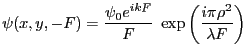
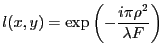
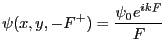
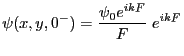

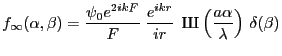
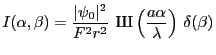
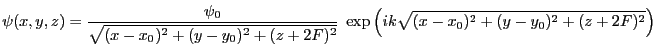
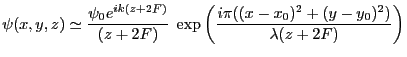
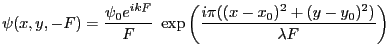
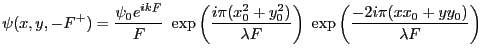
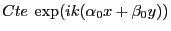 avec
avec
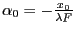 et
et
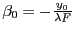
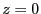 , il suffit de la multiplier par
, il suffit de la multiplier par
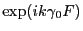 avec
avec
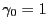 en optique paraxiale. Il vient
en optique paraxiale. Il vient
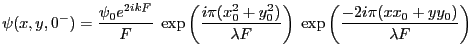
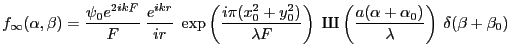
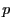 est donnée par les ``dents'' du peigne de Dirac ci-dessus. Il vient
est donnée par les ``dents'' du peigne de Dirac ci-dessus. Il vient
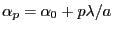 et
et
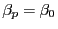 .
.
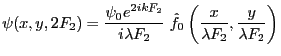

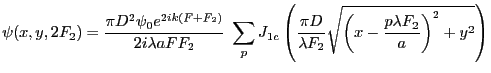
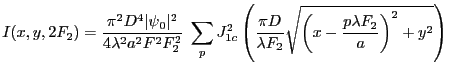
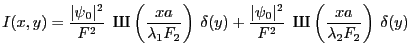
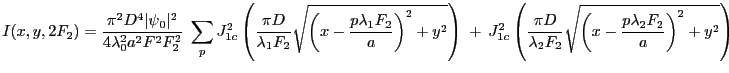
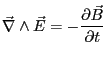
![$\displaystyle \displaystyle \vec\nabla \wedge \vec B=\mu_0[\sigma] \vec E+\mu_0\epsilon_0\frac{\partial \vec E}{\partial t}$](img89.png)
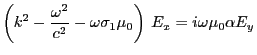
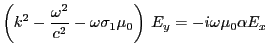
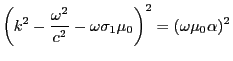
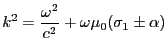
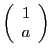 avec
avec 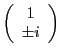 (déphasage de
(déphasage de 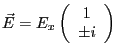 qui correspond à une polarisation circulaire (gauche ou droite). Ce sont donc ces ondes qui se propagent dans le milieu.
qui correspond à une polarisation circulaire (gauche ou droite). Ce sont donc ces ondes qui se propagent dans le milieu.
![$\displaystyle k=\frac{\omega}{c}\left[1+\frac{\sigma_1\pm\alpha}{\epsilon_0\omega} \right]^{1/2}
$](img113.png)
![$\displaystyle k\simeq\frac{\omega}{c}\left[1+\frac{\sigma_1\pm\alpha}{2\epsilon_0\omega} \right]
$](img117.png)
![$ \displaystyle n=\left[1+\frac{\sigma_1\pm\alpha}{2\epsilon_0\omega} \right]$](img118.png) .
Un des indices est celui de la vibration circulaire gauche, l'autre est
celui de la circulaire droite. Les vitesses de phase des ondes
s'obtiennent par
.
Un des indices est celui de la vibration circulaire gauche, l'autre est
celui de la circulaire droite. Les vitesses de phase des ondes
s'obtiennent par
![$ \displaystyle v=c/n\simeq c\left[1-\frac{\sigma_1\pm\alpha}{2\epsilon_0\omega} \right]$](img119.png)