L3 Physique -- Second partiel d'optique
19 Janvier 2011
Durée 2h
Documents autorisés : 1 feuille A4 manuscrite RV + formulaire de TF
Les deux exercices sont indépendants. N'oubliez pas de tourner la page, il y a des questions au verso.

![\includegraphics[width=5cm]{rochon.eps}](img18.png)
- Faire le tracé des rayons réfractés sur chaque face (construction de Descartes) et montrer qu'à la sortie du Rochon on a deux ondes planes polarisées linéairement.
- Ecrire les vecteurs d'onde
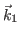 et
et 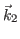 de ces deux ondes planes, et préciser leur direction de polarisation.
de ces deux ondes planes, et préciser leur direction de polarisation.
- Si
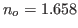 et
et 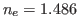 (cas de la calcite), peut-on utiliser l'approximation paraxiale pour ces deux ondes ?
(cas de la calcite), peut-on utiliser l'approximation paraxiale pour ces deux ondes ?
On s'intéresse maintenant à l'interférence entre les deux ondes sortant du Rochon. Le plan 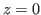 est pris juste à la sortie du Rochon, les franges sont observées dans un plan
est pris juste à la sortie du Rochon, les franges sont observées dans un plan 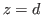 , en un point de coordonnées
, en un point de coordonnées  . On se place dans les conditions de l'optique paraxiale et on néglige les effets de bord (ce qui revient à considérer les deux ondes comme planes). On suppose en outre que les deux ondes sont d'amplitude égale
. On se place dans les conditions de l'optique paraxiale et on néglige les effets de bord (ce qui revient à considérer les deux ondes comme planes). On suppose en outre que les deux ondes sont d'amplitude égale  et qu'elles sont en phase à la sortie du Rochon. Le schéma est le suivant (attention les angles d'incidence des ondes 1 et 2 n'ont pas forcément été respectés sur le dessin).
et qu'elles sont en phase à la sortie du Rochon. Le schéma est le suivant (attention les angles d'incidence des ondes 1 et 2 n'ont pas forcément été respectés sur le dessin).
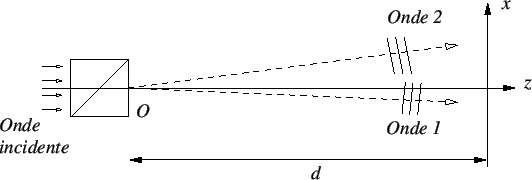
- Ecrire les vecteurs champs électriques
 et
et 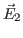 des deux ondes dans le plan
des deux ondes dans le plan 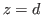
- Calculer l'intensité
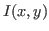 dans le plan
dans le plan 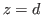 . Commentaires ?
. Commentaires ?
- Juste avant le plan
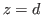 , on place un polariseur de direction
, on place un polariseur de direction
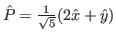 . Réécrire les deux champs électriques dans le plan
. Réécrire les deux champs électriques dans le plan 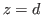 .
.
- Calculer la nouvelle intensité
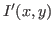 dans le plan
dans le plan 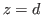
- Tracer le graphe de
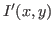 , préciser la valeur de l'interfrange et du contraste.
, préciser la valeur de l'interfrange et du contraste.
- Comment serait modifiée l'intensité
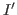 si l'onde était quasi-monochromatique, de fréquence centrale
si l'onde était quasi-monochromatique, de fréquence centrale 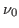 et de profil
et de profil
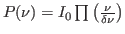 (on écrira, au préalable, l'intensité en fonction de la fréquence
(on écrira, au préalable, l'intensité en fonction de la fréquence 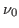 ).
).
On considère le schéma ci-dessous. Il s'agit d'un réseau de diffraction composé d'une grille de coefficient de transmission
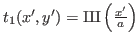 accolée à une fente carrée de côté
accolée à une fente carrée de côté 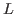 dans la direction
dans la direction 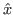 avec
avec 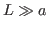 et supposée infinie dans la direction
et supposée infinie dans la direction 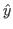 . Le plan du réseau est pris comme origine des
. Le plan du réseau est pris comme origine des 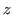 . Ce réseau est placé dans le plan focal objet d'une lentille convergente de focale
. Ce réseau est placé dans le plan focal objet d'une lentille convergente de focale 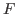 . L'éclairage est monochromatique, la longueur d'onde est
. L'éclairage est monochromatique, la longueur d'onde est 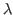 . On s'intéresse à l'intensité dans le plan focal image de la lentille.
. On s'intéresse à l'intensité dans le plan focal image de la lentille.
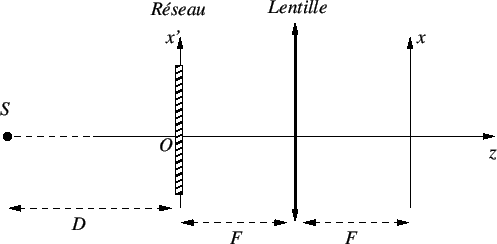
La source est ponctuelle et sur l'axe optique. Elle est située en 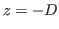 ,
, 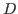 pouvant être considéré comme infini (approximation de Fraunhöffer). L'amplitude émise par la dans le plan
pouvant être considéré comme infini (approximation de Fraunhöffer). L'amplitude émise par la dans le plan 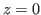 source est notée
source est notée  .
.
- Quelle est la nature de l'onde dans le plan
 , juste avant le réseau ?
, juste avant le réseau ?
- Ecrire l'amplitude complexe en sortie du réseau.
- En déduire l'intensité dans le plan
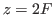 .
.
- Décrire l'image observée dans le plan
 et faire un dessin.
et faire un dessin.
- Pour un éclairage polychromatique, qu'appelle-t-on ``pouvoir de résolution'' du réseau ? Quelle est sa valeur dans l'ordre
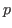 ?
?
- Calculer le rapport d'intensité entre l'ordre
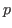 et l'ordre
et l'ordre 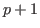 .
.
On déplace maintenant la source parallèlement à l'axe des 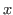 , de sorte qu'elle éclaire le réseau avec une incidende
, de sorte qu'elle éclaire le réseau avec une incidende 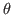 avec
avec
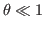 .
.
- Ecrire l'amplitude complexe en

- Ecrire l'intensité dans le plan
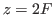 .
.
- Tracer le graphe de l'intensité en fonction de
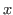 .
.
- Décrire en quelques mots l'effet du décalage de la source sur l'image dans le plan
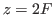 .
.
Le réseau est maintenant éclairé par deux sources ponctuelles identiques et incohérentes entre elles, situées toutes deux dans le plan 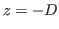 . L'une est sur l'axe optique, l'autre est décalée (incidende
. L'une est sur l'axe optique, l'autre est décalée (incidende 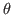 identique à la situation précédente).
identique à la situation précédente).
- Ecrire l'intensité dans le plan
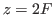 .
.
- Tracer le graphe de l'intensité en fonction de
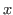 (se limiter aux ordres 0 à 2).
(se limiter aux ordres 0 à 2).
- A quelle condition sur
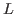 l'ordre
l'ordre 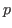 est-il séparé en deux images distinctes ? Cette condition dépend-elle de
est-il séparé en deux images distinctes ? Cette condition dépend-elle de 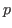 ?
?
La source est maintenant constituée d'un ensemble de 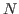 sources ponctuelles identiques
sources ponctuelles identiques 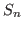 situées dans le plan
situées dans le plan 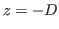 et alignées avec l'axe des
et alignées avec l'axe des 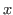 . Chaque source
. Chaque source 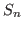 éclaire le réseau avec une incidence
éclaire le réseau avec une incidence 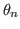 (avec
(avec 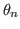 faible). On notera
faible). On notera 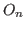 l'intensité produite par la source
l'intensité produite par la source 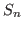 dans le plan
dans le plan  .
.
- Ecrire la distribution angulaire de brillance
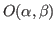 de la source sous la forme d'une somme.
de la source sous la forme d'une somme.
- En généralisant le résultat de la question 11, écrire l'intensité
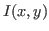 dans le plan
dans le plan 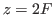

![\includegraphics[width=5cm]{rochon.eps}](img18.png)
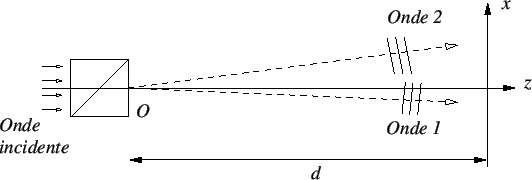

![]() ,
, ![]() pouvant être considéré comme infini (approximation de Fraunhöffer). L'amplitude émise par la dans le plan
pouvant être considéré comme infini (approximation de Fraunhöffer). L'amplitude émise par la dans le plan ![]() source est notée
source est notée ![]() .
.
![]() , de sorte qu'elle éclaire le réseau avec une incidende
, de sorte qu'elle éclaire le réseau avec une incidende ![]() avec
avec
![]() .
.
![]() . L'une est sur l'axe optique, l'autre est décalée (incidende
. L'une est sur l'axe optique, l'autre est décalée (incidende ![]() identique à la situation précédente).
identique à la situation précédente).
![]() sources ponctuelles identiques
sources ponctuelles identiques ![]() situées dans le plan
situées dans le plan ![]() et alignées avec l'axe des
et alignées avec l'axe des ![]() . Chaque source
. Chaque source ![]() éclaire le réseau avec une incidence
éclaire le réseau avec une incidence ![]() (avec
(avec ![]() faible). On notera
faible). On notera ![]() l'intensité produite par la source
l'intensité produite par la source ![]() dans le plan
dans le plan ![]() .
.