
![]()
![]()
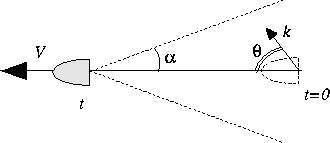
Pourquoi dans l'approximation faite, n'y a-t'il pas étalement du paquet d'ondes ? Quel est l'origine de cet étalement ?
![]()
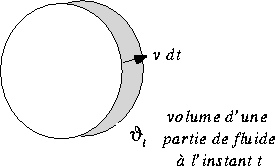
![]()
avec ![]() , on assimilera
, on assimilera ![]() à zéro.
à zéro.
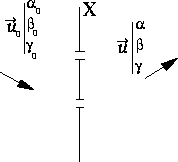
![]()
![]()
![]()
A est une constante. Cette onde se déplace vers les z>0.
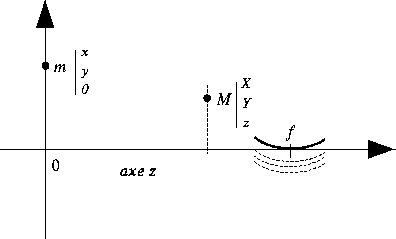
Dans la suite, on suppose
![]()
avec ![]() , et on admet, dans l'approximation de l'optique géométrique,
la formule suivante valable pour toute fonction d'une variable, par exemple
x, admettant des extréma en
, et on admet, dans l'approximation de l'optique géométrique,
la formule suivante valable pour toute fonction d'une variable, par exemple
x, admettant des extréma en ![]() :
:
![]()
le signe ![]() est le signe de
est le signe de ![]() . On observera que les intégrales sur x et y dans
le calcul de F(M). se factorisent.
. On observera que les intégrales sur x et y dans
le calcul de F(M). se factorisent.
![]()
c'est à dire si le rayon issu de ![]() passe par M.
passe par M.