Correction de l'examen d'optique
Session de Juin 2001
1. Une lentille éclairée
par une onde plane
-
L'intensité au foyer est une tache d'Airy (la lentille est de diamètre
a), le graphe est le suivant :
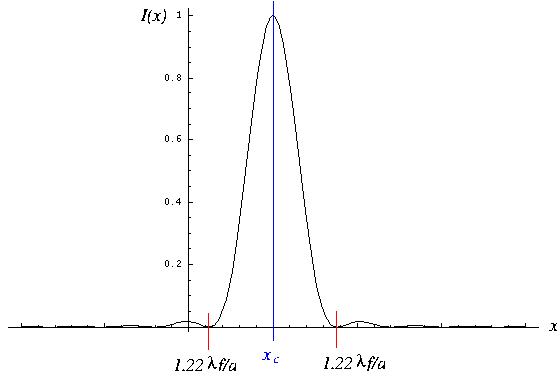
-

-
Taille
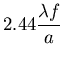 .
A.N : 2.44 microns
.
A.N : 2.44 microns
-
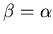 donc
donc 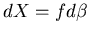 .
.
-
Si
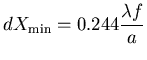 alors
alors 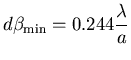 .
A.N. :
.
A.N. : 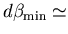 5 microradian
5 microradian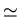 1 seconde d'arc.
1 seconde d'arc.
2. La lentille est éclairée
par une onde non plane
-
Soit
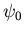 l'amplitude complexe à l'entrée de la lame (elle est constante
car l'onde arrive sous incidence normale sur la lame). A la sortie de la
lame (prise ici comme origine des z) elle s'écrit :
l'amplitude complexe à l'entrée de la lame (elle est constante
car l'onde arrive sous incidence normale sur la lame). A la sortie de la
lame (prise ici comme origine des z) elle s'écrit :
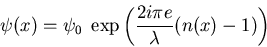
-
Nature de l'onde à la sortie de la lame (donc juste avant la lentille)
-
Si
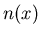 est constant l'onde est plane sous incidence normale (amplitude complexe
indépendante de
est constant l'onde est plane sous incidence normale (amplitude complexe
indépendante de 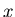 et
et 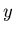 ).
).
-
Si
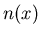 est linéaire l'onde est plane sous incidence oblique
est linéaire l'onde est plane sous incidence oblique
-
Si
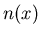 est quadratique l'onde est cylindrique (amplitude complexe de la forme
est quadratique l'onde est cylindrique (amplitude complexe de la forme 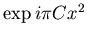 )
)
-
Si
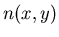 est quadratique en
est quadratique en 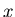 et en
et en 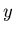 l'onde est sphérique (amplitude complexe de la forme
l'onde est sphérique (amplitude complexe de la forme 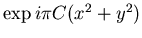 )
)
-
Pour
![$\displaystyle x\in \left[x_c-\frac{a}{2},x_c+\frac{a}{2}\right]$](img17.gif) on peut faire un développement limité de l'indice de réfraction
:
on peut faire un développement limité de l'indice de réfraction
:
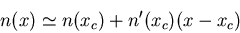
l'amplitude complexe à la sortie de la lame s'écrit alors
![\begin{displaymath}\begin{array}{ll}\psi(x)& \displaystyle =\psi_0 \; \exp\lef......{Cte} \; \exp \frac{2 i \pi}{\lambda} [n'(x_c) e] x\end{array}\end{displaymath}](img19.gif)
c'est une onde plane de vecteur d'onde 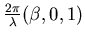 où
où 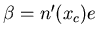 est la pente que fait le front d'onde avec le plan
est la pente que fait le front d'onde avec le plan  .
La réponse à la question est donc
.
La réponse à la question est donc
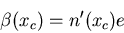
et donc la tache image au foyer de la lentille est centrée en
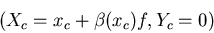
-
Si
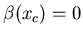 la lentille produit une image centrée en
la lentille produit une image centrée en 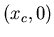 .
Si
.
Si 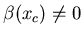 l'image se déplace d'une quantité
l'image se déplace d'une quantité 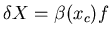 .
Si
.
Si 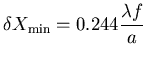 alors
alors 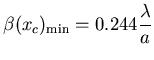 et on est dans le même cas que la question 1.5. On trouve
et on est dans le même cas que la question 1.5. On trouve
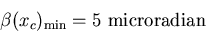
la plus petite valeur mesurable de la dérivée de l'indice
est alors

3. Analyseur de front d'onde
de Shack-Hartmann
-
Les images se forment sur les axes optiques de chaque lentille soit
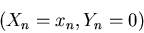
-
Comme pour la question 1.2 on trouve
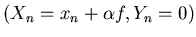 .
.
-
Même question que la 2.3 :
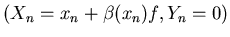
-
Supposons que l'on ait
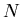 lentilles au total. On suppose que
lentilles au total. On suppose que 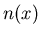 est une fonction continue, donc le front d'onde est aussi une fonction
continue. Soit
est une fonction continue, donc le front d'onde est aussi une fonction
continue. Soit 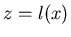 la fonction décrivant le front d'onde (surface sur laquelle l'amplitude
complexe est constante).
la fonction décrivant le front d'onde (surface sur laquelle l'amplitude
complexe est constante).
On a mesuré une collection 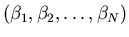 de pentes du front d'onde en des points
de pentes du front d'onde en des points 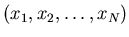 ,
avec
,
avec 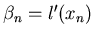 .
On a fait une approximation au premier ordre : sur chaque lentille la variation
d'indice est linéaire dont le front d'onde est plan. On peut alors
reconstruire graphiquement le front d'onde de la manière suivante
:
.
On a fait une approximation au premier ordre : sur chaque lentille la variation
d'indice est linéaire dont le front d'onde est plan. On peut alors
reconstruire graphiquement le front d'onde de la manière suivante
:
-
Entre
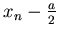 et
et 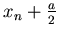 (donc sur la lentille numéro
(donc sur la lentille numéro 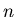 )
on va tracer un segment de droite de pente
)
on va tracer un segment de droite de pente 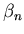 .
Ce segment de droite représente la courbe de
.
Ce segment de droite représente la courbe de  approximée au premier ordre
approximée au premier ordre
-
 étant continu, tous les segments de droite doivent se rejoindre
aux extrémités pour former une ligne brisée continue
étant continu, tous les segments de droite doivent se rejoindre
aux extrémités pour former une ligne brisée continue
-
cette méthode ne permet pas de mesurer la valeur de l'indice
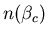 mais seulement sa dérivée ; on obtient la courbe de
mais seulement sa dérivée ; on obtient la courbe de  à une constante additive près (valeur de la phase sur le
front d'onde).
à une constante additive près (valeur de la phase sur le
front d'onde).

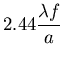 .
A.N : 2.44 microns
.
A.N : 2.44 microns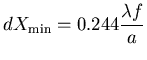 alors
alors 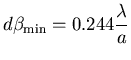 .
A.N. :
.
A.N. : 
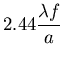 .
A.N : 2.44 microns
.
A.N : 2.44 microns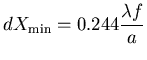 alors
alors 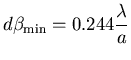 .
A.N. :
.
A.N. : ![$\displaystyle x\in \left[x_c-\frac{a}{2},x_c+\frac{a}{2}\right]$](img17.gif) on peut faire un développement limité de l'indice de réfraction
:
on peut faire un développement limité de l'indice de réfraction
:![\begin{displaymath}\begin{array}{ll}\psi(x)& \displaystyle =\psi_0 \; \exp\lef......{Cte} \; \exp \frac{2 i \pi}{\lambda} [n'(x_c) e] x\end{array}\end{displaymath}](img19.gif)
![]() où
où ![]() est la pente que fait le front d'onde avec le plan
est la pente que fait le front d'onde avec le plan ![]() .
La réponse à la question est donc
.
La réponse à la question est donc
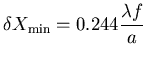 alors
alors 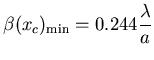 et on est dans le même cas que la question 1.5. On trouve
et on est dans le même cas que la question 1.5. On trouve![]() de pentes du front d'onde en des points
de pentes du front d'onde en des points ![]() ,
avec
,
avec ![]() .
On a fait une approximation au premier ordre : sur chaque lentille la variation
d'indice est linéaire dont le front d'onde est plan. On peut alors
reconstruire graphiquement le front d'onde de la manière suivante
:
.
On a fait une approximation au premier ordre : sur chaque lentille la variation
d'indice est linéaire dont le front d'onde est plan. On peut alors
reconstruire graphiquement le front d'onde de la manière suivante
: