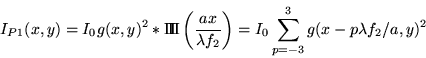-
Amplitude complexe juste avant la traversée de la lentille :
![\begin{displaymath}f_0(x,y)=\psi_0\; \prod\left(\frac{x}{a}\right) \prod\left(\......\; \left[ \delta(x-\frac{d}{2}) + \delta(x+\frac{d}{2})\right]\end{displaymath}](img1.gif)
Au foyer, l'amplitude est donnée par la TF de l'expression précédente
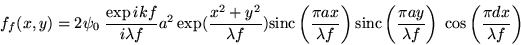
-
L'allure du plan focal est la suivante
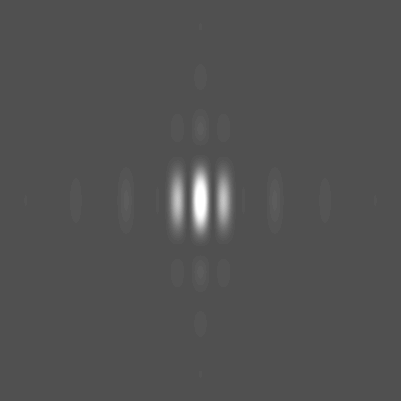
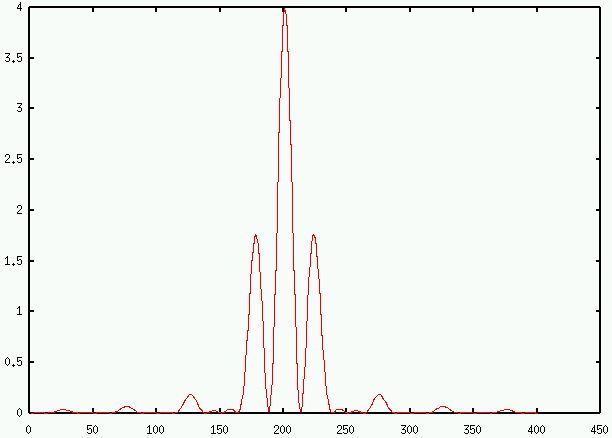
On observe des franges d'Young à l'intérieur d'une ta
che dûe à la diffraction par les trous. Le nombre de franges
visibles dans le lobe central est 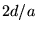 .
.
-
Le prisme dévie la lumière d'un angle égal à
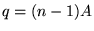 en optique paraxiale. Quand on met un tel prisme sur un des trous, l'onde
correspondant à ce trou est multipliée par un terme de phase
correspondant au coefficient de transmission du prisme. L'amplitude complexe
juste avant la lentille s'écrit
en optique paraxiale. Quand on met un tel prisme sur un des trous, l'onde
correspondant à ce trou est multipliée par un terme de phase
correspondant au coefficient de transmission du prisme. L'amplitude complexe
juste avant la lentille s'écrit
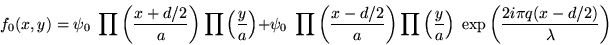
L'amplitude au plan focal s'écrit donc comme
![\begin{displaymath}f_f(x,y)= \psi_0\;\frac{\exp ikf}{i\lambda f} a^2 \mbox{sinc......)}{\lambda f}\right)\;\exp -\frac{i\pi d x}{\lambda f}\right]\end{displaymath}](img7.gif)
Lorsque 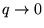 ,
on retombe sur la cas précédent : une fonction sinc striée
de franges. Le lobe central de ette fonction sinc étant de largeur
,
on retombe sur la cas précédent : une fonction sinc striée
de franges. Le lobe central de ette fonction sinc étant de largeur 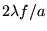 .
.
Dans le cas contraire, le terme entre crochets est constitué
de deux fonctions sinc, l'une centrée en 0 et l'autre en 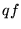 multipliées par des termes de phase conjugués. Lorsque
multipliées par des termes de phase conjugués. Lorsque 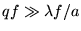 ,
les deux fonctions sinc du terme entre crochets ne se recouvrent pas ;
l'intensité s'approxime par la somme des carrés des modules
des deux termes (le double produit tend vers zéro) :
,
les deux fonctions sinc du terme entre crochets ne se recouvrent pas ;
l'intensité s'approxime par la somme des carrés des modules
des deux termes (le double produit tend vers zéro) :
![\begin{displaymath}I_f(x,y)\simeq \frac{\vert\psi_0\vert^2}{\lambda f} a^4 \mbo......box{sinc}^2\left(\frac{\pi a (x-qf)}{\lambda f}\right)\right]\end{displaymath}](img12.gif)
L'allure de la figure est la suivante : les franges ont disparu.

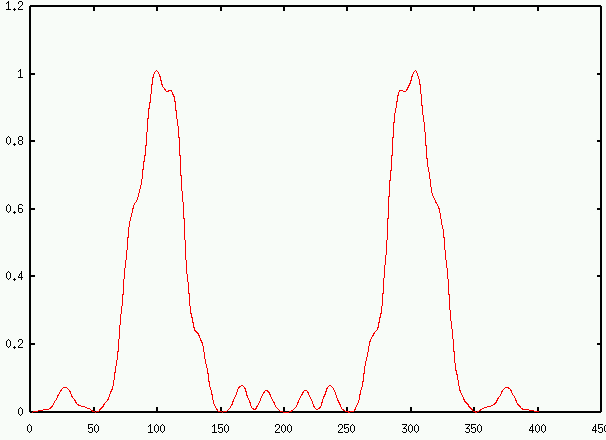
Lorsque 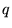 est inférieur et de l'ordre de
est inférieur et de l'ordre de 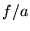 ,
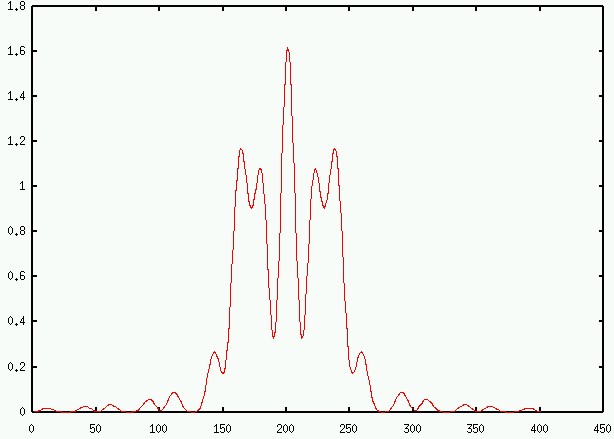
c'est le cas intermédiaire. Il y a recouvrement des termes entre
crochets, ce recouvrement est strié de franges. La figure ressemblerait
à celle-ci
,
c'est le cas intermédiaire. Il y a recouvrement des termes entre
crochets, ce recouvrement est strié de franges. La figure ressemblerait
à celle-ci

-
Dans le cas de deux lasers différents, on sait que les ondes provenant
de chacun de trous sont incohérentes entre elles. L'intensité
sera alors simplement la somme des deux intensités diffractées
par chacun des deux trous, soit simplement une tache en forme de sinc
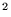 dans laquelle les franges d'interférences auront disparu.
dans laquelle les franges d'interférences auront disparu.
-
Au plan focal primaire
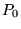 on observe une tache d'Airy. Si
on observe une tache d'Airy. Si 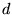 est le diamètre de l'objectif principal, le diamètre de son
premier anneau noir vaut
est le diamètre de l'objectif principal, le diamètre de son
premier anneau noir vaut

-
Si
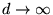 alors l'amplitude complexe tend vers une distribution
alors l'amplitude complexe tend vers une distribution 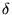 et s'écrit
et s'écrit
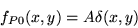
avec 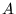 une constante. Cette amplitude est observée au foyer objet de la
collimatrice. Au foyer image de la collimatrice (là où se
trouve le réseau), on sait (cf cours sur le filtrage) que l'amplitude
est proportionnelle à la TF de
une constante. Cette amplitude est observée au foyer objet de la
collimatrice. Au foyer image de la collimatrice (là où se
trouve le réseau), on sait (cf cours sur le filtrage) que l'amplitude
est proportionnelle à la TF de 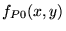 qui vaut
qui vaut 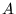 .
Donc sur le réseau, l'amplitude complexe est constante : l'onde
est plane sous incidence normale.
.
Donc sur le réseau, l'amplitude complexe est constante : l'onde
est plane sous incidence normale.
-
Si
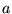 est la période du réseau, alors les différents ordres
font avec l'axe optique des angles
est la période du réseau, alors les différents ordres
font avec l'axe optique des angles 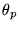 tels que
tels que
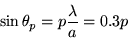
L'ordre maximum observable correspond à la condition 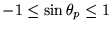 et on en tire
et on en tire 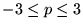 avec les valeurs numériques données.
avec les valeurs numériques données.
-
Si
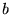 est la taille du réseau (carré),l'amplitude en sortie du
réseau s'écrit
est la taille du réseau (carré),l'amplitude en sortie du
réseau s'écrit
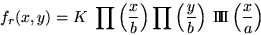
avec 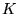 une constante.
une constante.
Le résean est dans le plan focal objet de la lentille de chambre,
le plan 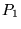 est le plan focal image de la même lentille ; l'amplitude complexe
dans le plan
est le plan focal image de la même lentille ; l'amplitude complexe
dans le plan 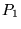 est donc donnée par
est donc donnée par
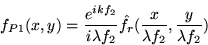
c'est à dire
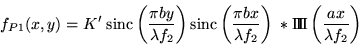
en mettant toutes les constantes dans 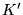 .
Si on pose
.
Si on pose 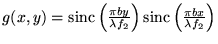 ,
alors l'intensité diffractée s'écrit (avec l'approximation
habituelle de non superposition des ordres)
,
alors l'intensité diffractée s'écrit (avec l'approximation
habituelle de non superposition des ordres)
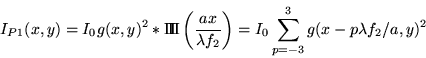
A l'ordre 0 (terme =p=0) : 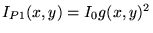 ,
c'est la tache de diffraction d'une ouverture carrée de côté
,
c'est la tache de diffraction d'une ouverture carrée de côté 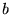 .
La taille du lobe central de cette figure est
.
La taille du lobe central de cette figure est 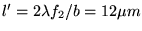 .
.
-
En totalité, nous avons 7 ordres observables, chacun donnant en
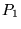 une tache identique à celle correspondant à l'ordre zéro.
Les différentes taches sont distantes de la quantité
une tache identique à celle correspondant à l'ordre zéro.
Les différentes taches sont distantes de la quantité 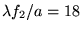 cm. Ce qui justifie a fortiori l'hypothèse de non-recouvrement des
différents ordres.
cm. Ce qui justifie a fortiori l'hypothèse de non-recouvrement des
différents ordres.


![]() .
.
![]() ,
on retombe sur la cas précédent : une fonction sinc striée
de franges. Le lobe central de ette fonction sinc étant de largeur
,
on retombe sur la cas précédent : une fonction sinc striée
de franges. Le lobe central de ette fonction sinc étant de largeur ![]() .
.
![]() multipliées par des termes de phase conjugués. Lorsque
multipliées par des termes de phase conjugués. Lorsque ![]() ,
les deux fonctions sinc du terme entre crochets ne se recouvrent pas ;
l'intensité s'approxime par la somme des carrés des modules
des deux termes (le double produit tend vers zéro) :
,
les deux fonctions sinc du terme entre crochets ne se recouvrent pas ;
l'intensité s'approxime par la somme des carrés des modules
des deux termes (le double produit tend vers zéro) :


![]() est inférieur et de l'ordre de
est inférieur et de l'ordre de ![]() ,
c'est le cas intermédiaire. Il y a recouvrement des termes entre
crochets, ce recouvrement est strié de franges. La figure ressemblerait
à celle-ci
,
c'est le cas intermédiaire. Il y a recouvrement des termes entre
crochets, ce recouvrement est strié de franges. La figure ressemblerait
à celle-ci