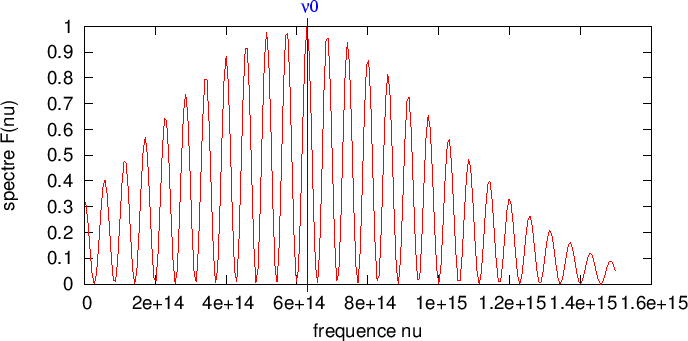
Les ondulations du spectre sont les cannelures. Le nombre de cannelures
est du même ordre que ![]() .
.
avec
et on somme sur
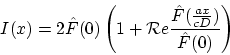
soit
avec

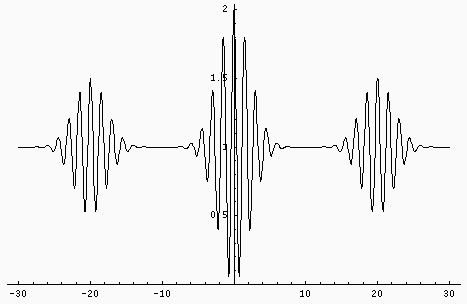
Session de Juin 2003

Les ondulations du spectre sont les cannelures. Le nombre de cannelures
est du même ordre que ![]() .
.
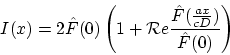


On peut choisir ou l'on veut l'origine des ![]() sans
changer l'intensité diffractée. Je choisis
sans
changer l'intensité diffractée. Je choisis
En posant ![]() et
et ![]() il vient (avec mes conventions pour les
il vient (avec mes conventions pour les ![]() )
)

Les coupes sur les axes s'écrivent :
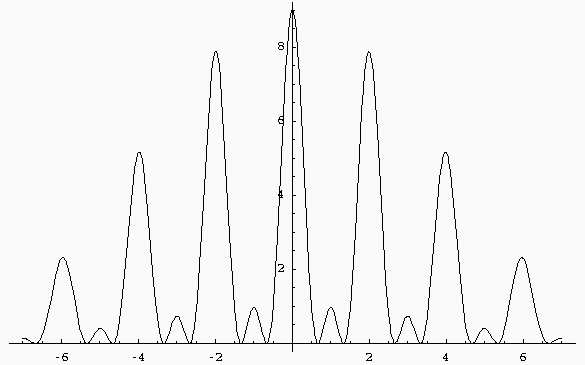
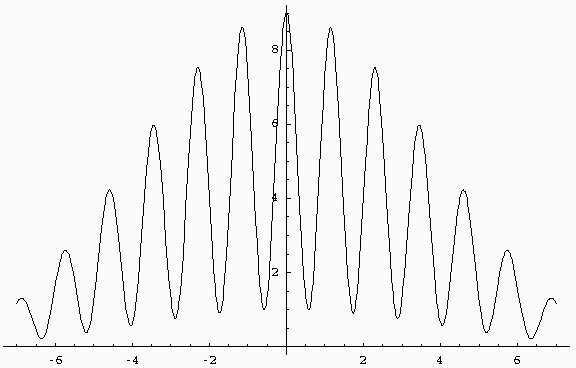
L'amplitude au centre s'écrit
annuler ![]() revient à annuler la somme de 3 nombres
complexes de module 1, ce qui est possible si les phases
revient à annuler la somme de 3 nombres
complexes de module 1, ce qui est possible si les phases ![]() sont
régulièrement réparties sur
sont
régulièrement réparties sur ![]() .
On peut prendre
.
On peut prendre ![]() ,
, ![]() et
et
![]() (les racines troisièmes de
l'unité). Donc un trou sans lame et deux trous avec des lames déphasant
de
(les racines troisièmes de
l'unité). Donc un trou sans lame et deux trous avec des lames déphasant
de ![]() et
et ![]()