- L'onde 2 arrive sur le miroir avec une incidence
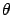 par rapport à sa normale. Elle en repart avec un
angle
par rapport à sa normale. Elle en repart avec un
angle 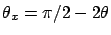 (avec la convention que
(avec la convention que 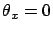 correspond à l'incidence normale). Posons
correspond à l'incidence normale). Posons
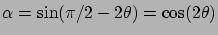 et
et
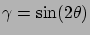 . Le vecteur d'onde de l'onde
2 a pour composantes
. Le vecteur d'onde de l'onde
2 a pour composantes 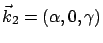 .
.
L'onde 2 a au point
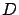 une amplitude complexe
une amplitude complexe
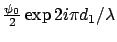 Elle s'écrira,
en un point
Elle s'écrira,
en un point 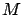 de coordonnées
de coordonnées 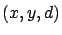 sur
l'écran
sur
l'écran 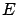 :
:

avec
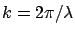 . L'intensité des franges d'interférences
s'écrit donc
. L'intensité des franges d'interférences
s'écrit donc
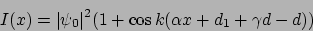
- Contraste 1, interfrange
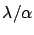 .
. 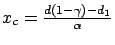
- Idée : remplacer
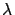 par
par 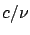 et
et 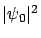 par
par
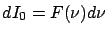 . Puis intégrer sur
. Puis intégrer sur 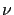 et faire apparaitre la partie réelle d'une TF. Il vient
et faire apparaitre la partie réelle d'une TF. Il vient
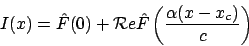
Le calcul de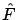 donne
donne

Finalement l'intensité des franges s'écrit
![\begin{displaymath}
I(x)=K \Delta\nu \; [1+C(x) \cos(k\alpha (x-x_c)) ]
\end{displaymath}](img25.png)
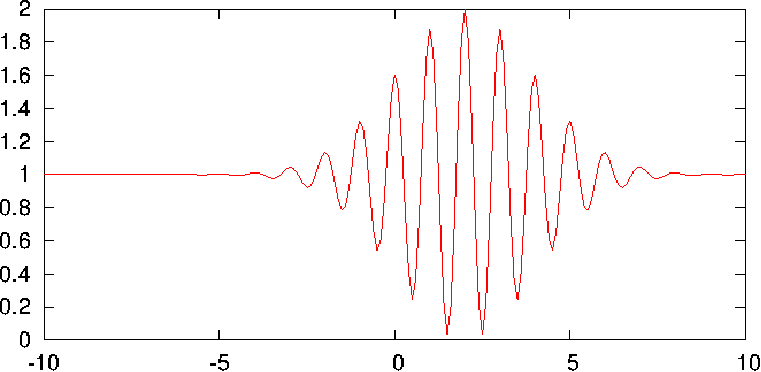
- Le contraste est

Gaussienne centrée sur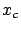 et de largeur de l'ordre de
et de largeur de l'ordre de
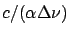 .
. - Intensité des franges pour
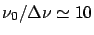
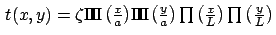 .
Il vient
.
Il vient
