LP2 - LPC4 : Examen partiel de Janvier 1998
Exercice
Un rayon lumineux arrive sous incidence normale sur un cristal uniaxe dont
l'axe Z parallèle au plan xz fait un angle  avec la normale à la surface de séparation. On suppose
avec la normale à la surface de séparation. On suppose  .
.

-
Rappeler comment on construit les rayons ordinaire et extraordinaire et
préciser sur le dessin les directions des vecteurs
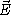 et
et  (on ne demande pas de calculs mais on donnera des explications précises
quant à cette construction).
(on ne demande pas de calculs mais on donnera des explications précises
quant à cette construction).
-
Le rayon incident étant polarisé elliptiquement comme
indiqué sur la figure 2 :

-
Justifier que les composantes du champ électrique s'écrivent
:


-
En faisant l'approximation
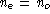 déterminer le rapport des intensités des rayons ordinaire
et extraordinaire.
déterminer le rapport des intensités des rayons ordinaire
et extraordinaire.
-
le cristal est taillé en lame à faces parallèles d'épaisseur
l.
-
Pourquoi les rayons sortants sont-ils parallèles à l'axe
z ?
-
Déterminer la différence de chemin optique relative
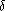 introduite par la lame pour ces deux rayons. On rappelle l'équation
introduite par la lame pour ces deux rayons. On rappelle l'équation

de la surface des vecteurs d'onde rapportée à la direction
Z de l'axe du cristal et une direction X qui lui est perpendiculaire.
On exprimera 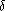 en fonction de
en fonction de 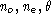 et l.
et l.
Problème : Interférences à N
trous en lumière cohérente et incohérente
Le but est de rétablir certains résultats vus en cours (ou
en TD) d'une manière (un peu) différente. Toutes les questions
peuvent être abordées indépendamment (à condition
de lire...et comprendre...l'énoncé).
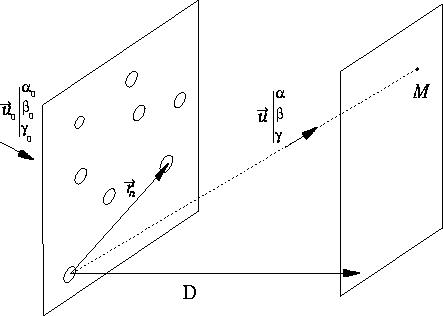
I. Une onde plane parfaitement cohérente (faisceau laser)
de longueur d'onde  , vecteur unitaire
, vecteur unitaire  éclaire un ensemble de N trous, considérés
comme ponctuels, situés dans le plan z=0 en des points de
coordonnées
éclaire un ensemble de N trous, considérés
comme ponctuels, situés dans le plan z=0 en des points de
coordonnées 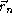 . On s'intéresse à l'intensité lumineuse ``à
l'infini'', en fait à grande distance D. Un point d'observation
M sera caractérisé par les composantes
. On s'intéresse à l'intensité lumineuse ``à
l'infini'', en fait à grande distance D. Un point d'observation
M sera caractérisé par les composantes  du vecteur unitaire de direction
du vecteur unitaire de direction  (cf. figure).
(cf. figure).
-
Montrer que si les trous sont identiques, l'intensité est proportionnelle
à :
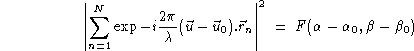
-
On considère des trous alignés selon Ox :
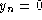 . Décrire, dans le plan
. Décrire, dans le plan 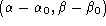 (
(  ,
,  fixés) l'intensité observée lorsque :
fixés) l'intensité observée lorsque :
-
On a deux trous séparés de a
-
On a N trous équidistants de a (N grand).
On posera  ; on rappelle que
; on rappelle que

-
Les trous sont situés en :

( 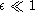 , N grand). En effectuant le développement
, N grand). En effectuant le développement

et en écrivant le sinus comme somme de deux exponentielles, montrer
l'existence de pics d'intensité supplémentaires (ghosts)
voisins de ceux établis en (b) (sauf près de  )
)
-
On considère des trous disposés aléatoirement autour
de O dans une région de dimension transverse
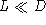 . L'expérience montre une figure de speckles dans le plan d'observation
considéré précédemment.
. L'expérience montre une figure de speckles dans le plan d'observation
considéré précédemment.
-
Qu'est-ce qu'une telle figure ?
-
Expliquer clairement pourquoi l'intensité en M varie
peu si
 (ou
(ou 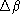 ) est inférieur ou égal à une quantité de l'ordre
de
) est inférieur ou égal à une quantité de l'ordre
de  .
.
-
Comparer la taille d'un speckle à la largeur de cohérence
en M de la lumière qui serait dûe à une source
incohérente de largeur L dans le plan z=0.
II. On éclaire les trous avec une source à l'infini,
incohérente, de longueur d'onde  , de répartition d'intensité
, de répartition d'intensité  . L'intensité observée dans la direction
. L'intensité observée dans la direction 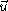 est notée
est notée  .
.
-
Qu'est-ce qu'une source (spatialement) incohérente ?
-
Les trous étant identiques, relier (à un coefficient
multiplicatif près) les fonctions I,
 et F
et F
-
En écrivant

et en posant
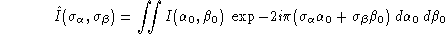
montrer que
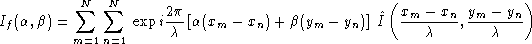
-
Interpréter le résultat obtenu en c en terme de filtrage
de la source par la pupille des N trous. Quelle est la fonction
de transfert ? (Question importante, bien détailler les explications)
-
Dans le cas de deux trous identiques alignés selon Ox et
distants de a, montrer que
 est périodique de période
est périodique de période 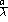 en
en  et a un contraste
et a un contraste

On rapellera la définition du constraste.
-
Pour une source circulaire, uniforme en intensité, centrée
dans la direction
 et de diamètre apparent
et de diamètre apparent 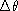 , pour quelle valeur minimale de a le contraste s'annule-t'il ?
Citer une application physique.
, pour quelle valeur minimale de a le contraste s'annule-t'il ?
Citer une application physique.
-
On considère le cas où les trous ne sont pas identiques et
où F s'écrit

-
Que peuvent prendre en compte le module et la phase de
 ?
?
-
Comment est modifiée la formule établie en 1 (c) ?
En déduire que pour une pupille continue, la fonction de transfert
est proportionnelle à la fonction d'autocorrélation

(on ne demande pas une démonstration mathématiquement
rigoureuse)



![]()
![]()
![]()
![]() en fonction de
en fonction de ![]() et l.
et l.![]() , vecteur unitaire
, vecteur unitaire ![]() éclaire un ensemble de N trous, considérés
comme ponctuels, situés dans le plan z=0 en des points de
coordonnées
éclaire un ensemble de N trous, considérés
comme ponctuels, situés dans le plan z=0 en des points de
coordonnées ![]() . On s'intéresse à l'intensité lumineuse ``à
l'infini'', en fait à grande distance D. Un point d'observation
M sera caractérisé par les composantes
. On s'intéresse à l'intensité lumineuse ``à
l'infini'', en fait à grande distance D. Un point d'observation
M sera caractérisé par les composantes ![]() du vecteur unitaire de direction
du vecteur unitaire de direction ![]() (cf. figure).
(cf. figure).

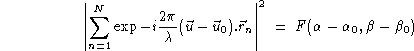

![]()
![]() , N grand). En effectuant le développement
, N grand). En effectuant le développement
![]()
![]() )
)![]()
![]()
![]()
![]()

![]()