L3 Physique -- Second partiel d'optique 2012-2013
durée 2h
Documents autorisés : une feuille A4 recto-verso manuscrite, formulaire de TF. Pas de calculatrice.
Le dispositif ci-dessous est un interféromètre de Mach-Zehnder. Il est constitué de deux miroirs parfaitement réfléchissants 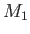 et
et 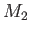 et et deux lames séparatrices identiques
et et deux lames séparatrices identiques 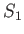 et
et 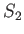 dont les coefficients de transmission et de réflexion en amplitude, de valeurs quelconques, sont notés respectivement
dont les coefficients de transmission et de réflexion en amplitude, de valeurs quelconques, sont notés respectivement 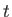 et
et 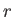 .
.
L'onde incidente, d'amplitude 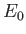 dans le plan
dans le plan  est plane et se propage parallèlement à l'axe
est plane et se propage parallèlement à l'axe 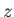 dans la direction des
dans la direction des 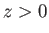 . Elle est divisée en deux ondes planes (notées 1 et 2) par
. Elle est divisée en deux ondes planes (notées 1 et 2) par 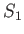 . L'onde 1 se réfléchit sur
. L'onde 1 se réfléchit sur 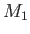 et traverse une lame à faces parallèles d'indice
et traverse une lame à faces parallèles d'indice 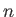 et d'épaisseur
et d'épaisseur 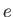 , avant de traverser
, avant de traverser 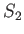 . On suppose que la lame à faces parallèles est parfaitement transparente et de dimension infinie. L'onde 2 se réfléchit sur
. On suppose que la lame à faces parallèles est parfaitement transparente et de dimension infinie. L'onde 2 se réfléchit sur 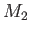 puis sur
puis sur 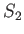 , et interfère ensuite avec l'onde 1. L'interférence est observée sur un écran noté
, et interfère ensuite avec l'onde 1. L'interférence est observée sur un écran noté 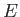 .
.
On note 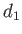 la distance entre l'origine et le centre de la première séparatrice
la distance entre l'origine et le centre de la première séparatrice 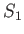 ,
, 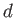 la distance
la distance 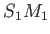 ,
, 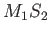 ,
, 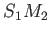 ,
,  et
et 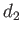 la distance
la distance 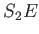 (voir schéma).
(voir schéma).
![\includegraphics[width=12cm]{mczender.eps}](img41.png)
Dans la première partie du problème, l'éclairage est monochromatique. La longueur d'onde est notée 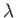 , la fréquence
, la fréquence 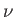 et l'amplitude complexe de l'onde dans le plan
et l'amplitude complexe de l'onde dans le plan  est
est 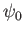 .
.
- Ecrire l'amplitude complexe de l'onde 2 sur l'écran
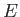 .
.
- Ecrire le coefficient de transmission
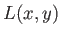 de la lame à faces parallèles se trouvant sur le trajet de l'onde
de la lame à faces parallèles se trouvant sur le trajet de l'onde 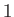 .
.
- Ecrire l'amplitude complexe de l'onde 1 sur l'écran
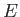 .
.
- Ecrire l'intensité sur l'écran
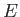 en fonction de la longueur d'onde
en fonction de la longueur d'onde 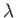 . Décrire l'image observée dans le plan
. Décrire l'image observée dans le plan 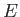 .
.
- A quelle condition sur
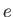 a-t-on une intensité nulle sur l'écran
a-t-on une intensité nulle sur l'écran 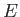 ?
?
- Donner le retard
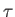 entre les ondes 1 et 2 et réécrire l'intensité en fonction de
entre les ondes 1 et 2 et réécrire l'intensité en fonction de 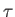 et de la fréquence
et de la fréquence 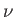 .
.
On considère maintenant une onde de spectre 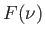 gaussien centré autour d'une fréquence
gaussien centré autour d'une fréquence 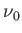 et de largeur de raie
et de largeur de raie  . Ce spectre s'écrit
. Ce spectre s'écrit
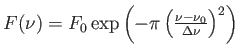 avec
avec
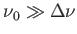 .
.
- Ecrire le profil de raie
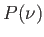 de cette onde.
de cette onde.
- Ecrire en fonction du retard
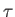 l'intensité
l'intensité 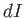 créée sur l'écran
créée sur l'écran 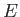 par une bande de fréquences
par une bande de fréquences
![$[\nu,\nu+d\nu]$](img35.png) .
.
- Ecrire en fonction du retard
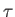 l'expression de l'intensité
l'expression de l'intensité 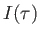 sur l'écran
sur l'écran 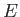
- On fait varier l'épaisseur
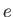 de la lame
de la lame 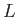 à partir de
à partir de  . Tracer la courbe de l'intensité en fonction de
. Tracer la courbe de l'intensité en fonction de 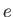 (mettre sur le graphe toutes les annotations qui vous paraissent pertinentes).
(mettre sur le graphe toutes les annotations qui vous paraissent pertinentes).
- Expliquer pourquoi les ondes 1 et 2 deviennent incohérentes entre elles quand
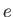 devient grand (il n'est pas demandé de calcul).
devient grand (il n'est pas demandé de calcul).
- Donner un ordre de grandeur de la valeur maximale
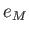 que peut prendre
que peut prendre 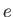 pour que les ondes 1 et 2 soient cohérentes entre elles. Ecrire
pour que les ondes 1 et 2 soient cohérentes entre elles. Ecrire 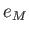 en fonction de la longueur de cohérence
en fonction de la longueur de cohérence 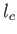 .
.
- A partir du résultat de la question 8, expliquer pourquoi certaines fréquences sont éteintes à la sortie de l'interféromètre (on parle de ``spectre cannelé''). Ecrire les fréquences manquantes en fonction de
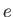 et donner en fonction de
et donner en fonction de  un ordre de grandeur du nombre de cannelures dans le spectre de l'onde (dépendance de
un ordre de grandeur du nombre de cannelures dans le spectre de l'onde (dépendance de 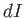 avec
avec 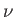 ) dans le plan
) dans le plan 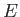 .
.
Une étoile supposée ponctuelle est entourée d'un anneau de matière circulaire qui émet de la lumière. L'ensemble étoile+anneau constitue une source spatialement incohérente monochromatique (longueur d'onde 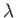 ) dont la distribution angulaire de brillance est représentée par la fonction
) dont la distribution angulaire de brillance est représentée par la fonction
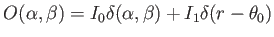 avec
avec
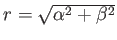 . On suppose que
. On suppose que 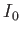 ,
, 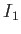 et
et 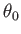 sont positifs avec
sont positifs avec 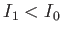 (étoile plus brillante que l'anneau).
Cette source est observée par un interféromètre à deux télescopes de base
(étoile plus brillante que l'anneau).
Cette source est observée par un interféromètre à deux télescopes de base 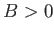 orientés parallèlement à la direction
orientés parallèlement à la direction 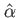 . Ces deux télescopes sont assimilables à des trous d'Young comme dans le schéma ci-dessous. On note
. Ces deux télescopes sont assimilables à des trous d'Young comme dans le schéma ci-dessous. On note 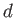 la distance entre le plan des trous et le plan d'observation des franges (
la distance entre le plan des trous et le plan d'observation des franges (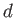 est assez grand pour faire l'approximation de Fraunhofer entre le plan des trous et le plan des franges).
est assez grand pour faire l'approximation de Fraunhofer entre le plan des trous et le plan des franges).
![\includegraphics[width=10cm]{cspat.eps}](img67.png)
- Rappeler la condition sur
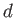 ,
, 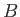 et
et 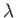 pour que l'on puisse faire l'approximation de Fraunhofer entre le plan des trous et le plan des franges
pour que l'on puisse faire l'approximation de Fraunhofer entre le plan des trous et le plan des franges
- Rappeler ce qu'est une source spatialement incohérente.
- Rappeler la signification physique de la largeur de cohérence spatiale
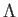 et donner son expression dans le cas de cette source étoile+anneau.
et donner son expression dans le cas de cette source étoile+anneau.
- Calculer le degré complexe de cohérence spatiale
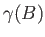 . On pourra simplifier l'expression en considérant
. On pourra simplifier l'expression en considérant 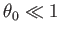 .
.
- En déduire le contraste
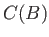 des franges d'Young.
des franges d'Young.
- A l'aide de la table de
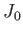 ci-après donner, en fonction de
ci-après donner, en fonction de 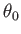 , la première valeur
, la première valeur 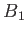 de
de 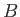 pour laquelle le contraste passe par un minimum (on rappelle que
pour laquelle le contraste passe par un minimum (on rappelle que 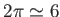 ).
).
- Rappeler ce qu'on appelle ``inversion de contraste''. Avec les hypothèses de l'énoncé, ce phénomène s'observe-t'il ici (justifiez votre réponse) et si oui, pour quelles valeurs de
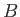 ?
?
- Ecrire l'intensité des franges d'Young
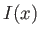 .
.
- Tracer le graphe de
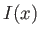 dans 2 cas :
dans 2 cas : 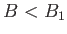 et
et 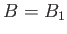 . Portez sur votre graphe toutes les annotations pertinentes.
. Portez sur votre graphe toutes les annotations pertinentes.
- On observe le premier minimum de contraste pour
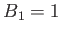 m en observant à la longueur d'onde
m en observant à la longueur d'onde 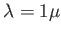 m. Quel est alors le diamètre angulaire de l'anneau de matière autour de l'étoile (on rappelle que 1 seconde d'arc=5.
m. Quel est alors le diamètre angulaire de l'anneau de matière autour de l'étoile (on rappelle que 1 seconde d'arc=5. 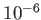 rad).
rad).
Table de valeurs de la fonction de Bessel 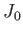 |
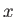 |
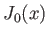 |
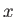 |
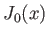 |
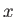 |
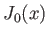 |
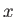 |
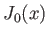 |
| 0.0 |
1.00 |
1.8 |
0.34 |
3.6 |
-0.39 |
5.4 |
-0.04 |
| 0.1 |
0.99 |
1.9 |
0.28 |
3.7 |
-0.39 |
5.5 |
-0.00 |
| 0.2 |
0.99 |
2.0 |
0.22 |
3.8 |
-0.40 |
5.6 |
0.02 |
| 0.3 |
0.97 |
2.1 |
0.16 |
3.9 |
-0.40 |
5.7 |
0.05 |
| 0.4 |
0.96 |
2.2 |
0.11 |
4.0 |
-0.39 |
5.8 |
0.09 |
| 0.5 |
0.93 |
2.3 |
0.05 |
4.1 |
-0.38 |
5.9 |
0.12 |
| 0.6 |
0.91 |
2.4 |
0.00 |
4.2 |
-0.37 |
6.0 |
0.15 |
| 0.7 |
0.88 |
2.5 |
-0.04 |
4.3 |
-0.36 |
6.1 |
0.17 |
| 0.8 |
0.84 |
2.6 |
-0.09 |
4.4 |
-0.34 |
6.2 |
0.20 |
| 0.9 |
0.80 |
2.7 |
-0.14 |
4.5 |
-0.32 |
6.3 |
0.22 |
| 1.0 |
0.76 |
2.8 |
-0.18 |
4.6 |
-0.29 |
6.4 |
0.24 |
| 1.1 |
0.71 |
2.9 |
-0.22 |
4.7 |
-0.26 |
6.5 |
0.26 |
| 1.2 |
0.67 |
3.0 |
-0.26 |
4.8 |
-0.24 |
6.6 |
0.27 |
| 1.3 |
0.62 |
3.1 |
-0.29 |
4.9 |
-0.20 |
6.7 |
0.28 |
| 1.4 |
0.56 |
3.2 |
-0.32 |
5.0 |
-0.17 |
6.8 |
0.29 |
| 1.5 |
0.51 |
3.3 |
-0.34 |
5.1 |
-0.14 |
6.9 |
0.29 |
| 1.6 |
0.45 |
3.4 |
-0.36 |
5.2 |
-0.11 |
7.0 |
0.30 |
| 1.7 |
0.39 |
3.5 |
-0.38 |
5.3 |
-0.07 |
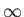 |
0.00 |
![]() dans le plan
dans le plan ![]() est plane et se propage parallèlement à l'axe
est plane et se propage parallèlement à l'axe ![]() dans la direction des
dans la direction des ![]() . Elle est divisée en deux ondes planes (notées 1 et 2) par
. Elle est divisée en deux ondes planes (notées 1 et 2) par ![]() . L'onde 1 se réfléchit sur
. L'onde 1 se réfléchit sur ![]() et traverse une lame à faces parallèles d'indice
et traverse une lame à faces parallèles d'indice ![]() et d'épaisseur
et d'épaisseur ![]() , avant de traverser
, avant de traverser ![]() . On suppose que la lame à faces parallèles est parfaitement transparente et de dimension infinie. L'onde 2 se réfléchit sur
. On suppose que la lame à faces parallèles est parfaitement transparente et de dimension infinie. L'onde 2 se réfléchit sur ![]() puis sur
puis sur ![]() , et interfère ensuite avec l'onde 1. L'interférence est observée sur un écran noté
, et interfère ensuite avec l'onde 1. L'interférence est observée sur un écran noté ![]() .
.
![]() la distance entre l'origine et le centre de la première séparatrice
la distance entre l'origine et le centre de la première séparatrice ![]() ,
, ![]() la distance
la distance ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() la distance
la distance ![]() (voir schéma).
(voir schéma).
![\includegraphics[width=12cm]{mczender.eps}](img41.png)
![]() , la fréquence
, la fréquence ![]() et l'amplitude complexe de l'onde dans le plan
et l'amplitude complexe de l'onde dans le plan ![]() est
est ![]() .
.
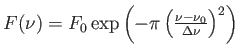 avec
avec
![\includegraphics[width=10cm]{cspat.eps}](img67.png)