Le 2e prisme a une épaisseur ![]() , dans l'intervalle
, dans l'intervalle ![]() . Le coefficient de transmission associé est
. Le coefficient de transmission associé est
![]() .
.
Le coefficient de transmission de l'ensemble, incluant la limitation à l'intervalle ![]() est donc :
est donc :
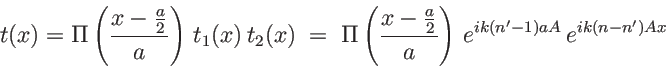
4 Mars 2015
Le 2e prisme a une épaisseur ![]() , dans l'intervalle
, dans l'intervalle ![]() . Le coefficient de transmission associé est
. Le coefficient de transmission associé est
![]() .
.
Le coefficient de transmission de l'ensemble, incluant la limitation à l'intervalle ![]() est donc :
est donc :
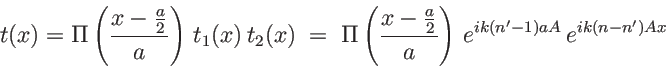
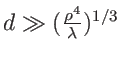 avec
avec
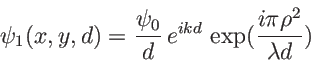
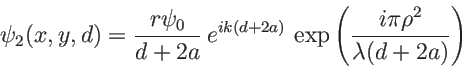
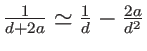 . Ce développement peut-ètre simplifié à
. Ce développement peut-ètre simplifié à 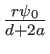 . Il vient
. Il vient
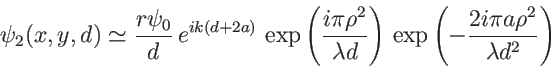
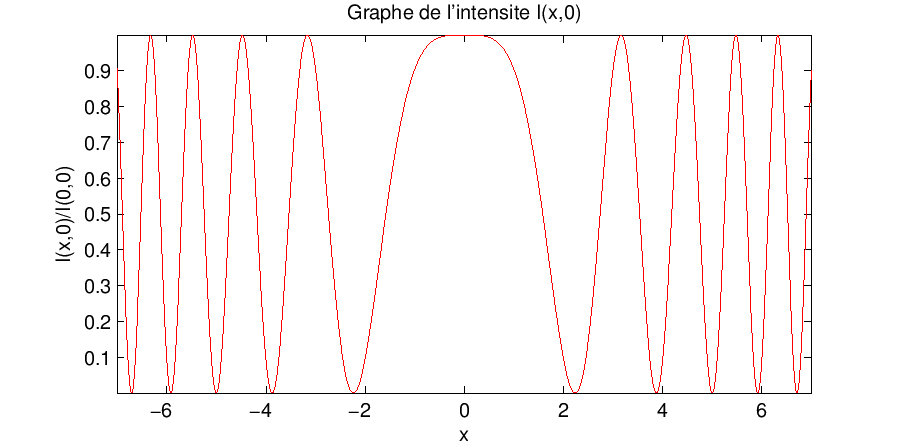
![\begin{displaymath}
I(x,y)=\frac{\vert\psi_0\vert^2 (1+r^2)}{d^2}\, \left[1+\fr...
...a}{\lambda} \left(\frac{\rho^2}{2d^2}-1\right) \right)\right]
\end{displaymath}](img29.png)
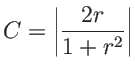 . Lorsque
. Lorsque
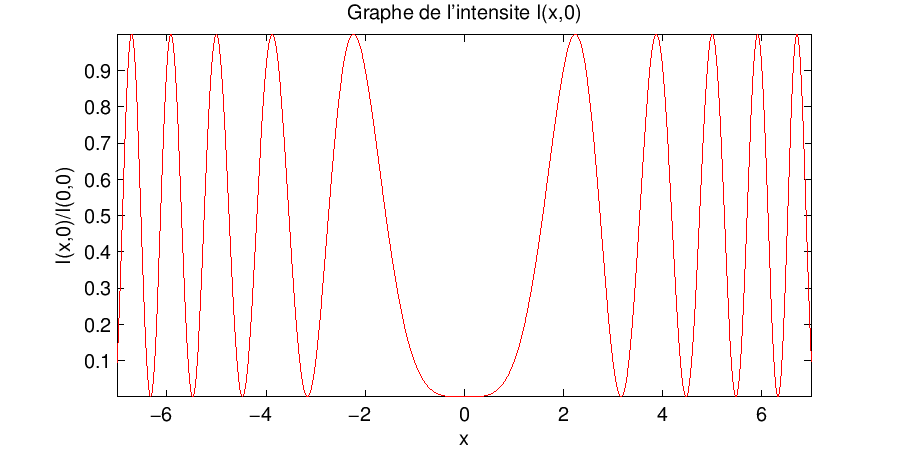
![\begin{displaymath}
I(x,y)=\frac{\vert\psi_0\vert^2 (1+r^2)}{d^2}\, \left[1+\fr...
...{1+r^2} \, \cos\left(2\pi N \frac{\rho^2}{d^2} \right)\right]
\end{displaymath}](img39.png)
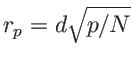 avec
avec
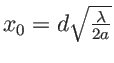
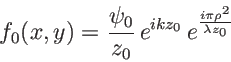
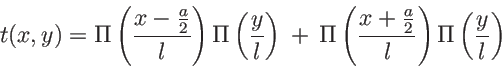
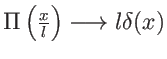 . Il vient
. Il vient
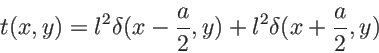
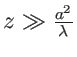
![\begin{displaymath}
f_{0+}(x,y)=f_0(x,y)\, t(x,y) \;=\; \frac{\psi_0 l^2}{z_0}\...
...mbda z_0}}\: [ \delta(x-\frac a 2,y) + \delta(x+\frac a 2,y)]
\end{displaymath}](img64.png)
et en utilisant l'identité
![]() il vient
il vient
![\begin{displaymath}
f_{0+}(x,y)={\psi_0 l^2}{z_0}\, e^{ikz_0}\, e^{\frac{i\pi a...
...bda z_0}} \: [ \delta(x-\frac a 2,y) + \delta(x+\frac a 2,y)]
\end{displaymath}](img66.png)
Dans la suite on posera
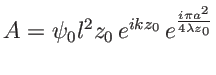 . L'amplitude complexe en
. L'amplitude complexe en ![]() s'écrit, dans l'approximation de Fraunhofer
s'écrit, dans l'approximation de Fraunhofer

le calcul donne
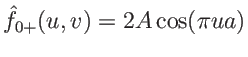 . On a donc
. On a donc
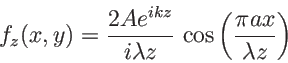
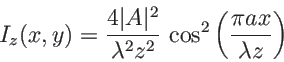
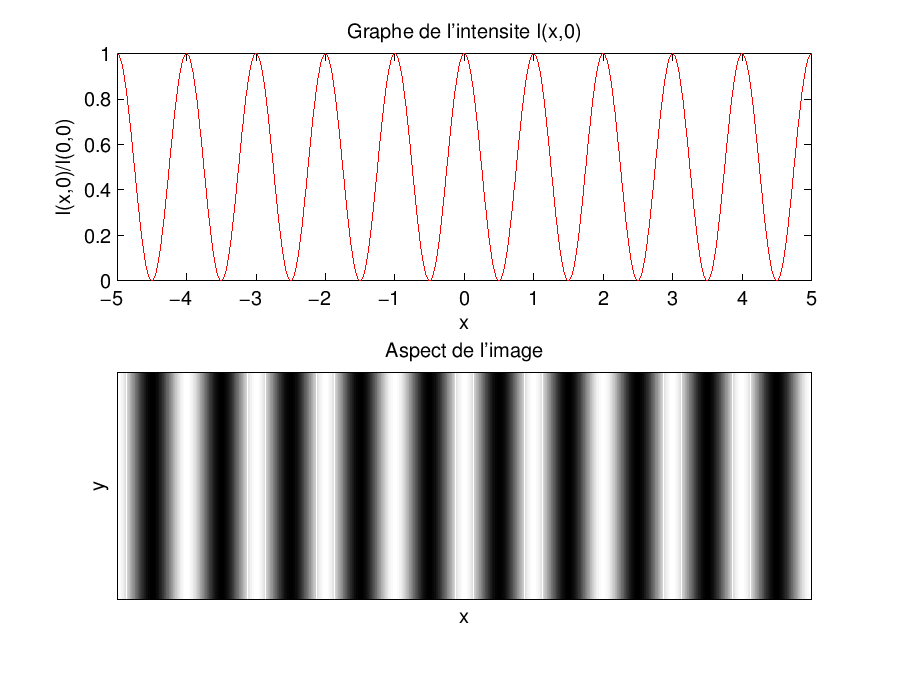
![\begin{displaymath}
f_{0+}(x,y)={\psi_0}{z_0}\, e^{ikz_0}\, \, e^{\frac{i\pi\rh...
...c{x+\frac a 2}{l}\right)\Pi\left(\frac{y}{l}\right)
\right]
\end{displaymath}](img77.png)
Dans ce cas le calcul de la TF de ![]() intervenant dans l'expression de l'amplitude
intervenant dans l'expression de l'amplitude ![]() fait intervenir un produit de convolution :
fait intervenir un produit de convolution :
![\begin{displaymath}
\hat f_{0+}(u,v)=C^{te} TF\left[ e^{\frac{i\pi\rho^2}{\lamb...
...c{x+\frac a 2}{l}\right)\Pi\left(\frac{y}{l}\right)
\right]
\end{displaymath}](img80.png)
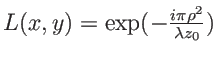 L'ensemble lentille+masque a donc pour coefficient de transmission le produit de
L'ensemble lentille+masque a donc pour coefficient de transmission le produit de ![\begin{displaymath}
t_2(x,y)=\exp(-\frac{i\pi\rho^2}{\lambda z_0})\: \left[\Pi\...
...rac{x+\frac a 2}{l}\right)\Pi\left(\frac{y}{l}\right) \right]
\end{displaymath}](img85.png)
![\begin{displaymath}
f_{0+}(x,y)={\psi_0}{z_0}\, e^{ikz_0}\, \, e^{\frac{i\pi\rh...
...{l}\right)
\right] \; \exp(-\frac{i\pi\rho^2}{\lambda z_0})
\end{displaymath}](img86.png)
![\begin{displaymath}
f_{0+}(x,y)={\psi_0}{z_0}\, e^{ikz_0}\,\left[
\Pi\left(\f...
...c{x+\frac a 2}{l}\right)\Pi\left(\frac{y}{l}\right)
\right]
\end{displaymath}](img87.png)
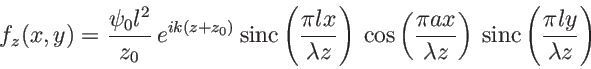
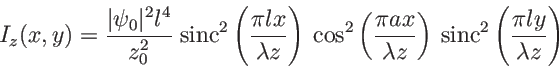
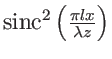 ).
).