Correction du premier Partiel
14 Novembre 2008
- La période est
 . Pour le coefficient de transmission les trois expressions suivantes sont valables :
. Pour le coefficient de transmission les trois expressions suivantes sont valables :
- On met
 sous forme d'une série de Fourier (formule de Poisson). Il vient
sous forme d'une série de Fourier (formule de Poisson). Il vient
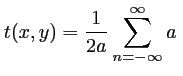
sinc

l'amplitude complexe  en
en  s'écrit donc, en faisant apparaitre
s'écrit donc, en faisant apparaitre  :
:
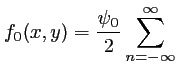
sinc

on reconnait une somme d'ondes planes dans le plan  caractérisées par des directions
caractérisées par des directions

- La TF du coefficient de transmission s'écrit
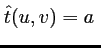
sinc

donc l'intensité diffractée à l'infini s'écrit
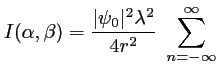
sinc

- Les ordres
 pairs ``tombent'' sur les zéros du sinc, ils annulent le coefficient
sinc
pairs ``tombent'' sur les zéros du sinc, ils annulent le coefficient
sinc sauf l'ordre
sauf l'ordre  . Ils sont absents de la figure de diffraction.
. Ils sont absents de la figure de diffraction.
- L'intensité est infinie pour
 (présence d'un
(présence d'un
 ). On trace en fait ce qui est en facteur de
). On trace en fait ce qui est en facteur de
 , c'est à dire la quantité
, c'est à dire la quantité
 sinc
sinc qui décrit la dépendance de l'intensité avec
qui décrit la dépendance de l'intensité avec  sur l'axe
sur l'axe  .
.
![\includegraphics[width=17cm]{sinc2.eps}](img41.gif)
- L'ordre maximal observable est donné par la condition
 car
car  est un sinus. Avec les valeurs numériques celà donne
est un sinus. Avec les valeurs numériques celà donne  mais comme les ordres pairs sont éteints on a donc
mais comme les ordres pairs sont éteints on a donc  et 9 pics observables (les impairs de -7 à 7 plus le zéro).
et 9 pics observables (les impairs de -7 à 7 plus le zéro).
- La largeur des portes devient
 . La période du réseau est inchangée donc
. La période du réseau est inchangée donc  aussi. L'intensité s'écrit
aussi. L'intensité s'écrit
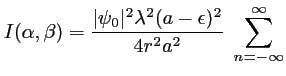
sinc

Cette fois les ordres pairs sont observables car ils ``tombent'' légèrement à côté des zéros du sinc.
- Si le réseau est tronqué le coefficient de transmission
 est multiplié par une porte
est multiplié par une porte  . L'amplitude diffractée est convoluée par
. L'amplitude diffractée est convoluée par
 sinc
sinc , chaque pic de Dirac est alors remplacé par ce sinc. La condition
, chaque pic de Dirac est alors remplacé par ce sinc. La condition  assure que les sinc ne se recouvrent pas. L'intensité diffractée s'écrit
assure que les sinc ne se recouvrent pas. L'intensité diffractée s'écrit
Le pouvoir de résolution dans l'ordre  est
est
 (à écrire sans démonstration).
(à écrire sans démonstration).

![\includegraphics[width=5cm]{fente1.eps}](img55.gif)
- Amplitude dans le plan
 :
:
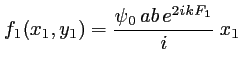
sinc

ce qui se simplifie en utilisant la relation
sinc :
:
- L'intensité s'écrit
Comme dans l'exercice 1, on trace  en omettant le terme
en omettant le terme
 .
.
![\includegraphics[width=18cm]{sin2.eps}](img56.gif)
- Dans le plan
 l'amplitude s'écrit
l'amplitude s'écrit
Les deux pics de Dirac ne sont pas dans le même sens, celui de droite (situé en
 ) est négatif.
) est négatif.
- Intensité :
![\includegraphics[width=14cm]{2delta.eps}](img57.gif)
- En sortie de la lame, les deux pics de Diracs sont dans le même sens (négatifs tous les deux) :
- Amplitude dans le plan
 :
:
ce sont des franges du même type que celles produites par des fentes de Young.
- Intensité dans le plan

Au centre de la figure l'intensité est maximale (frange brillante).
![\includegraphics[width=18cm]{cos2.eps}](img63.gif)
- Contraste 1. Fréquences spatiales : 0,


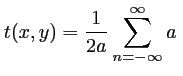 sinc
sinc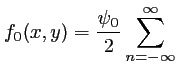 sinc
sinc
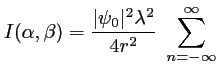 sinc
sinc sinc
sinc![\includegraphics[width=17cm]{sinc2.eps}](img41.gif)
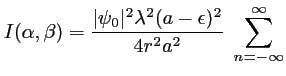 sinc
sinc
 sinc
sinc

![\includegraphics[width=5cm]{fente1.eps}](img55.gif)
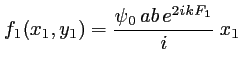 sinc
sinc


![\includegraphics[width=18cm]{sin2.eps}](img56.gif)


![\includegraphics[width=14cm]{2delta.eps}](img57.gif)



![\includegraphics[width=18cm]{cos2.eps}](img63.gif)
