Correction du premier partiel d'optique
3 Novembre 2009
---------
- Le coefficient de transmission doit être sans dimension. La quantité
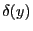 est l'inverse d'une longueur,
est l'inverse d'une longueur, 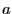 est donc sans dimension.
est donc sans dimension.
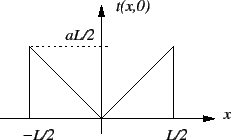
- Le masque placé dans le plan
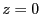 est de taille
est de taille 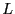 ; l'approximation du champ lointain est donc valable quand
; l'approximation du champ lointain est donc valable quand
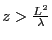
- Diffraction à l'infini
- Graphe
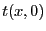 .
.
-
![$ \displaystyle t(x,y)=\frac{aL}{2}\left[\Pi\left(\frac x L\right)-\Lambda\left(\frac {x} {L/2}\right)\right]\delta(y)$](img8.png)
- Amplitude à l'infini :
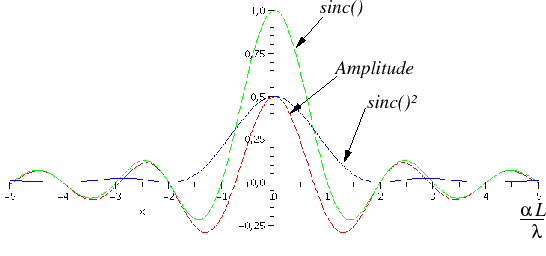
- Le sinc
 est deux fois plus large que le sinc : les deux fonctions s'annulent simultanément en
est deux fois plus large que le sinc : les deux fonctions s'annulent simultanément en
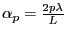 . L'allure du graphe est celle de la courbe ci-dessous. On a tracé simultanément les fonctions
sinc
. L'allure du graphe est celle de la courbe ci-dessous. On a tracé simultanément les fonctions
sinc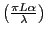 ,
,
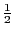 sinc
sinc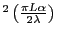 et l'amplitude (avec
et l'amplitude (avec
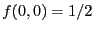 ).
).
- Diffraction de Fresnel sur l'axe optique
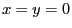 .
.
- On part de la transformée de Fourier-Fresnel que l'on écrit en
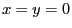 . Cette transformée s'écrit
. Cette transformée s'écrit
et se simplifie si l'on fait 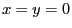 en
en
et comme la transformée de Fourier, prise en (0,0), est simplement l'intégrale de la fonction, on obtient
L'intégrale sur 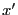 est limitée entre
est limitée entre 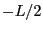 et
et 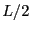 (présence de la porte). Quant à celle sur
(présence de la porte). Quant à celle sur 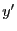 elle fait simplement 1 (le produit
elle fait simplement 1 (le produit
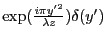 vaut
vaut
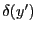 ). On obtient la forme intégrale demandée :
). On obtient la forme intégrale demandée :
- Pour calculer l'intégrale, on se sert du fait que la dérivée de
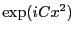 vaut
vaut
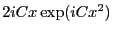 . La primitive de
. La primitive de
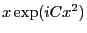 vaut donc
vaut donc
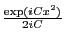 . Il vient
. Il vient
On a donc
- L'intensité est
avec
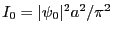 On a une annulation de l'intensité tous les
On a une annulation de l'intensité tous les
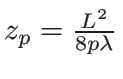 . Plus
. Plus 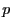 augmente plus
augmente plus 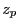 diminue ; le point le plus éloigné où l'intensité est nulle au centre (hormis p=0) est
diminue ; le point le plus éloigné où l'intensité est nulle au centre (hormis p=0) est
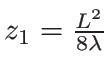 , c'est le même ordre de grandeur que la limite entre le champ proche et le champ lointain (
, c'est le même ordre de grandeur que la limite entre le champ proche et le champ lointain (
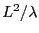 ).
).
- Le coefficient de transmission de la lame est
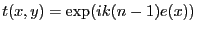 avec
avec
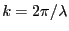 . Il vient
. Il vient
avec
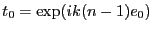 . Si
. Si
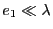 le produit
le produit
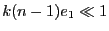 et l'on peut faire un développement limité de l'exponentielle. Il vient :
et l'on peut faire un développement limité de l'exponentielle. Il vient :
L'amplitude diffractée à l'infini (distance 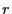 ) s'écrit
) s'écrit
avec
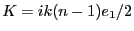 et
et
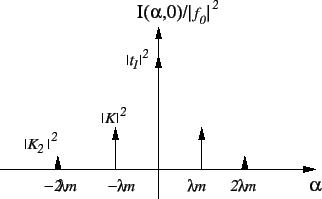
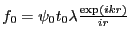 . L'amplitude (et donc l'intensité) est composée de 3 pics de Diracs centrés en
. L'amplitude (et donc l'intensité) est composée de 3 pics de Diracs centrés en 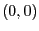 ,
,
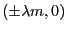 dans le plan
dans le plan
 . Ce sont les ordres 0 et
. Ce sont les ordres 0 et 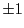 .
.
- Second ordre
- On pousse le développement limité de l'exponentielle à l'ordre 2. Il vient
- L'amplitude diffractée à l'infini s'écrit donc
avec
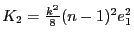
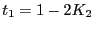 . L'intensité s'écrit donc
. L'intensité s'écrit donc
- Par rapport à la question 1 il y a deux différences : l'apparition de deux nouveaux ordres en
 , et un changement dans le coefficient qui pondère l'ordre 0.
, et un changement dans le coefficient qui pondère l'ordre 0.
- Rapport d'intensité :
- La limite
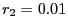 donne
donne
 . Pour
. Pour 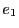 plus petit que cette valeur le DL à l'ordre 1 suffit.
plus petit que cette valeur le DL à l'ordre 1 suffit.
- Généralisation à
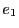 quelconque : le développement en série de l'exponentielle conduit à écrire
quelconque : le développement en série de l'exponentielle conduit à écrire 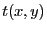 comme une somme
comme une somme
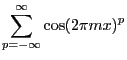 . L'écriture du cosinus en deux exponentielles complexes fait apparaitre des termes de type
. L'écriture du cosinus en deux exponentielles complexes fait apparaitre des termes de type
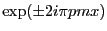 qui donneront naissance dans l'amplitude à des pics de Dirac centrés en
qui donneront naissance dans l'amplitude à des pics de Dirac centrés en
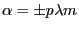 : ce sont les ordres
: ce sont les ordres 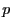 et
et 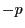 .
.
- C'est une question de cours. L'ordre maximal observable
est donné par la formule des réseaux (le sinus de l'angle de déviation
ne peut être supérieur à 1). L'ordre
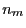 correspondant est donné par
correspondant est donné par
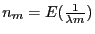 (
(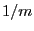 est ici la période du réseau). Il vient
est ici la période du réseau). Il vient 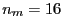 .
.
 .
.
![$ \displaystyle t(x,y)=\frac{aL}{2}\left[\Pi\left(\frac x L\right)-\Lambda\left(\frac {x} {L/2}\right)\right]\delta(y)$](img8.png)

![$\displaystyle f(\alpha,\beta)=a L^2 \psi_0\frac{\exp(ikr)}{2 i \lambda r}\: \left...
...right)-\frac 1 2\mbox{sinc}^2\left(\frac{\pi L\alpha}{2 \lambda}\right)\right]
$](img10.png)
 est deux fois plus large que le sinc : les deux fonctions s'annulent simultanément en
est deux fois plus large que le sinc : les deux fonctions s'annulent simultanément en
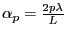 . L'allure du graphe est celle de la courbe ci-dessous. On a tracé simultanément les fonctions
sinc
. L'allure du graphe est celle de la courbe ci-dessous. On a tracé simultanément les fonctions
sinc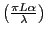 ,
,
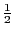 sinc
sinc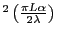 et l'amplitude (avec
et l'amplitude (avec
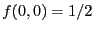 ).
).
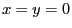 . Cette transformée s'écrit
. Cette transformée s'écrit
![$\displaystyle f_z(x,y)=\psi_0\frac{\exp(ikz)}{i \lambda z}\: \exp\left(i\pi\fra...
...a z}}\left[ t(x',y') \exp\left(i\pi\frac{x'^2+y'^2}{\lambda z} \right)
\right]
$](img19.png)
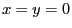 en
en
![$\displaystyle f_z(0,0)=\psi_0\frac{\exp(ikz)}{i \lambda z}\: {\cal F}_{0,0}\left[ t(x',y') \exp\left(i\pi\frac{x'^2+y'^2}{\lambda z} \right)
\right]
$](img20.png)
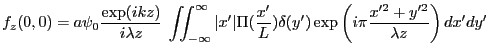
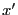 est limitée entre
est limitée entre 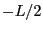 et
et 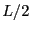 (présence de la porte). Quant à celle sur
(présence de la porte). Quant à celle sur 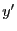 elle fait simplement 1 (le produit
elle fait simplement 1 (le produit
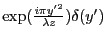 vaut
vaut
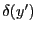 ). On obtient la forme intégrale demandée :
). On obtient la forme intégrale demandée :
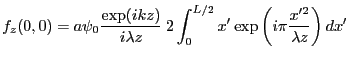
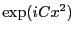 vaut
vaut
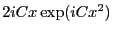 . La primitive de
. La primitive de
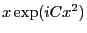 vaut donc
vaut donc
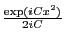 . Il vient
. Il vient
![$\displaystyle f_z(0,0)=a\psi_0\frac{\exp(ikz)}{i \lambda z}\: \frac{2\lambda z}{2 i \pi}\left[\exp\left(i\pi\frac{x'^2}{\lambda z}\right) \right]_0^{L/2}
$](img33.png)
![$\displaystyle f_z(0,0)=-\psi_0\exp(ikz)\: \frac{a}{\pi}\left[\exp\left(i\pi\frac{L^2}{4 \lambda z}\right) -1\right]
$](img34.png)
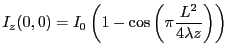
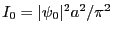 On a une annulation de l'intensité tous les
On a une annulation de l'intensité tous les
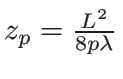 . Plus
. Plus 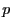 augmente plus
augmente plus 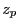 diminue ; le point le plus éloigné où l'intensité est nulle au centre (hormis p=0) est
diminue ; le point le plus éloigné où l'intensité est nulle au centre (hormis p=0) est
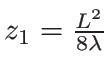 , c'est le même ordre de grandeur que la limite entre le champ proche et le champ lointain (
, c'est le même ordre de grandeur que la limite entre le champ proche et le champ lointain (
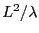 ).
).
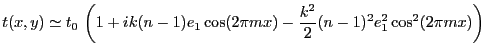
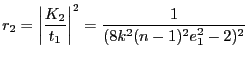
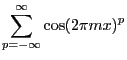 . L'écriture du cosinus en deux exponentielles complexes fait apparaitre des termes de type
. L'écriture du cosinus en deux exponentielles complexes fait apparaitre des termes de type