L3 Physique -- Correction du premier partiel d'optique
19 Octobre 2010
On note 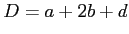 et
et
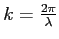
-
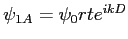 et
et
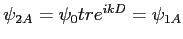 . Intensité :
. Intensité :
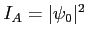
-
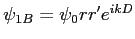 et
et
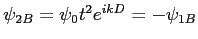 . Intensité :
. Intensité : 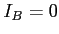
- L'intensité est la puissance/unité de surface. Elle est constante dans chaque plan, donc conserver la puissance revient à conserver l'intensité. A l'entrée de l'interféromètre l'intensité dans le plan
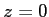 est
est
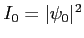 . A la sortie l'intensité totale est la somme
. A la sortie l'intensité totale est la somme
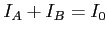 . Il y a bien conservation de l'intensité donc de la puissance lumineuse. Dans ce cas, l'éclairement du plan
. Il y a bien conservation de l'intensité donc de la puissance lumineuse. Dans ce cas, l'éclairement du plan 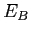 est nul et toute la lumière est allée vers le plan
est nul et toute la lumière est allée vers le plan 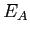 .
.
- On note
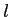 le coefficient de transmission de la lame à faces parallèles
le coefficient de transmission de la lame à faces parallèles
-
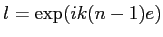
-
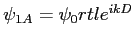 et
et
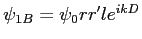
-
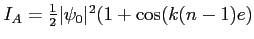 et
et
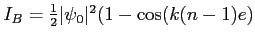 . Avec
. Avec
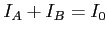 , la puissance lumineuse est toujours conservée.
, la puissance lumineuse est toujours conservée.
-
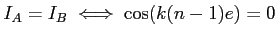 . Ce qui donne
. Ce qui donne
 avec
avec 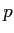 entier.
entier.
-
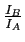 peut s'écrire comme
peut s'écrire comme
On aura
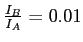 quand
quand
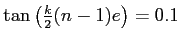 donc
donc
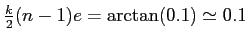 . Ce qui donne
. Ce qui donne
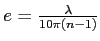 . A.N.
. A.N.
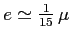 m.
m.
- Oui, la justification étant donnée par la réponse à la question précédente (une épaisseur de
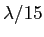 donne un rapport d'intensité de 1% entre
donne un rapport d'intensité de 1% entre 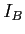 et
et 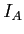 qui est facilement mesurable).
qui est facilement mesurable).
- Eclairé par une onde plane, cet objet ne laisse passer la lumière que sur une mince fente infiniment fine : son aspect est celui d'un fil lumineux, d'où le titre de l'exercice.
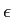 est homogène à une longueur pour que
est homogène à une longueur pour que 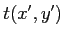 soit sans dimension (
soit sans dimension (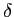 est homogène à l'inverse de son argument).
est homogène à l'inverse de son argument).
-
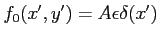 ou bien
ou bien
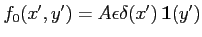
-
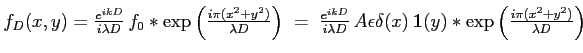
- Les fonctions sont à variables séparables,
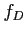 s'exprime comme le produit d'un terme ne dépendant que de
s'exprime comme le produit d'un terme ne dépendant que de 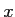 par un terme ne dépendant que de
par un terme ne dépendant que de 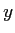 :
:
qui s'écrit
l'intégrale sur 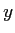 vaut
vaut
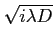 . On obtient
. On obtient
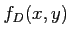 ne dépend pas de
ne dépend pas de 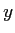 . C'est une onde cylindrique.
. C'est une onde cylindrique.
-
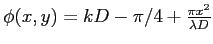 (le
(le 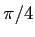 vient du
vient du 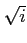 au dénominateur).
au dénominateur).
-
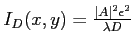 (elle est constante et homogène à
(elle est constante et homogène à  )
)
- Dans le plan
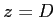 , l'amplitude complexe de l'onde plane s'écrit
, l'amplitude complexe de l'onde plane s'écrit
 . L'amplitude complexe résultant de son interférence avec
. L'amplitude complexe résultant de son interférence avec 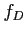 s'écrit
s'écrit
- L'intensité correspondante dans le cas où
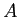 et
et 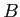 sont réels et
sont réels et
 est
est
- Maxima d'intensité en
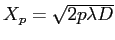 ; minima en
; minima en
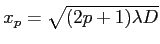 avec
avec 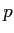 entier
entier
- Contraste
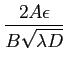
- Graphe de l'intensité
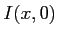 en fonction de
en fonction de 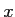 : les valeurs numériques utilisées sont
: les valeurs numériques utilisées sont
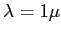 m,
m, 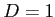 cm,
cm, 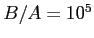 ,
,

![\includegraphics[width=15cm]{intens.eps}](img70.gif)
- La phase
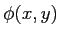 de l'onde
de l'onde 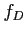 vaut
vaut
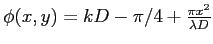 : c'est, à une constante additive près, l'argument du cosinus qui intervient dans l'intensité.
: c'est, à une constante additive près, l'argument du cosinus qui intervient dans l'intensité.
- Une solution possible est d'éclairer l'interféromètre de Michelson avec une onde plane sous incidence normale. Les deux miroirs sont réglés en teinte plate (pas d'inclinaison). Sur l'un des miroirs (par exemple
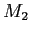 ), on place une fente fine (collée au miroir) : l'onde réfléchie sera une onde cylindrique qui pourra interférer avec l'onde plane provenant de
), on place une fente fine (collée au miroir) : l'onde réfléchie sera une onde cylindrique qui pourra interférer avec l'onde plane provenant de 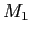 .
.
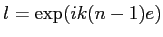
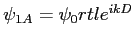 et
et
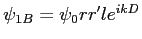
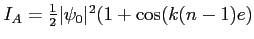 et
et
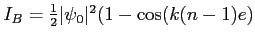 . Avec
. Avec
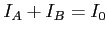 , la puissance lumineuse est toujours conservée.
, la puissance lumineuse est toujours conservée.
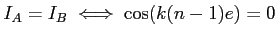 . Ce qui donne
. Ce qui donne
 avec
avec 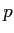 entier.
entier.
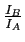 peut s'écrire comme
peut s'écrire comme
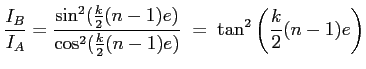
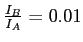 quand
quand
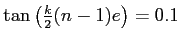 donc
donc
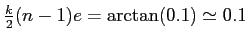 . Ce qui donne
. Ce qui donne
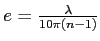 . A.N.
. A.N.
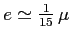 m.
m.
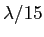 donne un rapport d'intensité de 1% entre
donne un rapport d'intensité de 1% entre 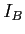 et
et 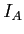 qui est facilement mesurable).
qui est facilement mesurable).
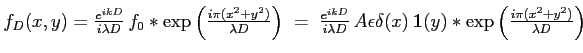
![$\displaystyle f_D(x,y)= \frac{e^{ikD}}{i\lambda D} \, A\epsilon \left[\delta(x)...
...].\left[\mathbf{1}(y) \ast \exp\left(\frac{i \pi y^2}{\lambda D}\right)\right]
$](img42.gif)
![$\displaystyle f_D(x,y)= \frac{e^{ikD}}{i\lambda D} \, A\epsilon \; \exp\left(\f...
...t[\int_{-\infty}^\infty \exp\left(\frac{i \pi y^2}{\lambda D}\right) dy\right]
$](img43.gif)
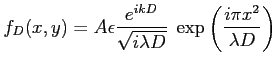
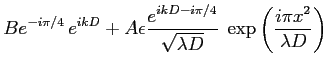
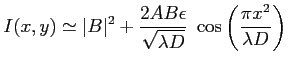
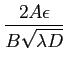
![\includegraphics[width=15cm]{intens.eps}](img70.gif)