Correction de l'examen d'optique de Septembre 2003
Rédaction libre. Je conseille de présenter la cohérence
spatiale à travers une expérience d'interférences de
type trous d'Young (même si c'est en réalité plus général).
Les points importants sont :
- On travaille avec des sources larges. Introduire la notion de distribution
de brillance.
- L'émission de lumière est faire indépendemment
par chaque point de la source, on doit donc sommer les intensités
des franges produites par tous ces points
- Plus la source est large et plus les franges perdent du contraste.
Le contraste des franges est une mesure du degré de cohérence
spatiale de l'onde produite par la source. On peut citer ici le théorème
de Van-Cittert-Zernike qui relie le contraste des franges à la distribution
de brillance.
- Pour une source de dimensions données, le contraste des franges
baisse quand on écarte les trous d'Young. A partir d'un certain écartement
le contraste est quasi-nul et les deux trous sont quasiment incohérents
entre eux. Cette écartement critique est la largeur de cohérence
spatiale de l'onde. Donner sa définition exacte.
- Enfin terminer par des applications : mesure de diamètres d'étoiles,
etc...
Le coefficient de transmission du trou s'écrit
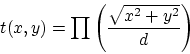
On écrit la transformée de Fresnel de l'onde après traversée
du masque ; l'amplitude complexe s'écrit
![\begin{displaymath}
f_z(x,y)=\frac{\exp ikz}{i\lambda z}\; \exp\left(\frac{x^2+y...
...(x',y') \: \exp\left(\frac{x'^2+y'^2}{\lambda z}\right)\right]
\end{displaymath}](img2.png)
On fait 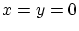 , on développe la TF, on trouve l'intégrale
sur la surface du diaphragme
, on développe la TF, on trouve l'intégrale
sur la surface du diaphragme
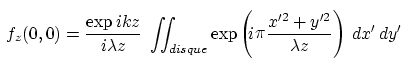
qu'on intègre en coordonnées polaires. On trouve finalement
l'intensité sur l'axe optique (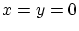 ) :
) :
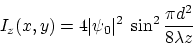
L'intensité s'annule pour les valeurs
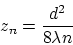
avec 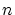 entier. Dans ce cas la figure de diffraction de
Fresnel montre une tache noire d'intensité nulle au centre.
entier. Dans ce cas la figure de diffraction de
Fresnel montre une tache noire d'intensité nulle au centre.
- Si
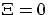 on a affaire à une lame à faces
parallèles
on a affaire à une lame à faces
parallèles
- Période du réseau :
- Comme pour tous les réseaux, l'ordre
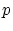 est observé
dans la direction de cosinus directeur
est observé
dans la direction de cosinus directeur
- Le pouvoir de résolution est
- Fonction épaisseur du motif (on centre le motif à l'origine)
Coefficient de transmission du motif (on le limite par une porte de largeur
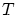 )
)
Le coefficient de transmission du réseau est la périodisée
de 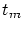
avec 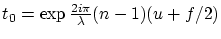 et
et
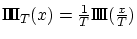
- TF de
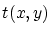
Amplitude diffractée à l'infini
D'où l'intensité (en écrivant
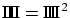 )
)
C'est à dire un peigne de Dirac dont les dents sont situées
en  (ce
sont les ordres) et pondérées par la fonction sinc
(ce
sont les ordres) et pondérées par la fonction sinc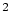 qui est centrée en
qui est centrée en 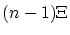 . Lorsque
. Lorsque 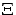 varie, le sinc se décale et l'amplitude des ordres change.
varie, le sinc se décale et l'amplitude des ordres change.
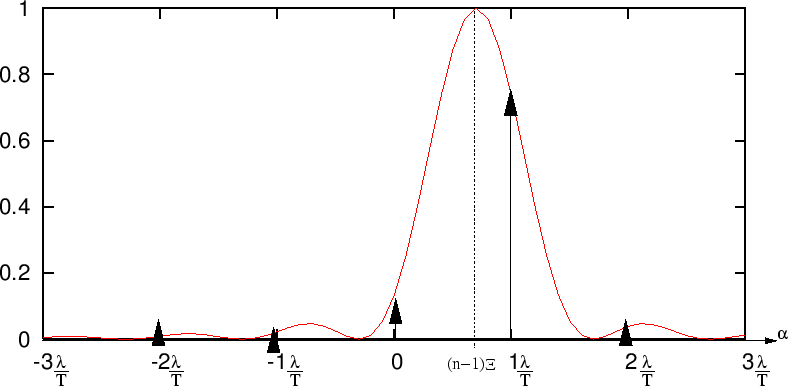
- Les zéros de la fonction sinc
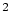 sont situés
en
sont situés
en 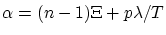 avec
avec 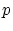 entier non nul. On
constate alors que si
entier non nul. On
constate alors que si 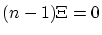 toutes les dents du peigne
(donc tous les ordres) sauf l'ordre 0 ont une amplitude nulle (ils ``tombent''
sur les zéros du sinc). Dans ce sas seul l'ordre 0 est observable.
Si
toutes les dents du peigne
(donc tous les ordres) sauf l'ordre 0 ont une amplitude nulle (ils ``tombent''
sur les zéros du sinc). Dans ce sas seul l'ordre 0 est observable.
Si 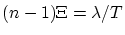 c'est
l'ordre 1 seul qui est observable, tous les autres sont d'amplitude nulle.
Et si
c'est
l'ordre 1 seul qui est observable, tous les autres sont d'amplitude nulle.
Et si 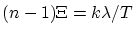 avec
avec
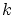 entier, seul l'ordre
entier, seul l'ordre 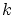 est observable.
est observable.
- Réseau blasé dans l'ordre
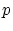 si
si
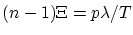 . Ici
. Ici 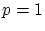 , avec
les valeurs proposées on trouve
, avec
les valeurs proposées on trouve 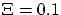 rad.
rad.
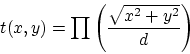
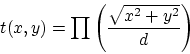
![\begin{displaymath}
f_z(x,y)=\frac{\exp ikz}{i\lambda z}\; \exp\left(\frac{x^2+y...
...(x',y') \: \exp\left(\frac{x'^2+y'^2}{\lambda z}\right)\right]
\end{displaymath}](img2.png)