Interférences avec un
spectre cannelé
On considère une lumière de spectre cannelé 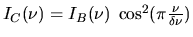 ,
on désigne par
,
on désigne par 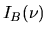 le spectre de la lumière blanche. On effectue une expérience
d'interférences pour laquelle le contraste en lumière monochromatique
est 1 (trous d'Young par exemple, ou interféromètre de Michelson).
le spectre de la lumière blanche. On effectue une expérience
d'interférences pour laquelle le contraste en lumière monochromatique
est 1 (trous d'Young par exemple, ou interféromètre de Michelson).
-
1.
-
Calculer et représenter le contraste des franges d'interférences
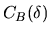 pour la lumière blanche (
pour la lumière blanche (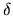 est la différence de chemin optique). On modélisera pour
simplifier le spectre
est la différence de chemin optique). On modélisera pour
simplifier le spectre 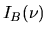 de la lumière blanche par une gaussienne de largeur
de la lumière blanche par une gaussienne de largeur 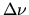 centrée en
centrée en 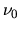 .
.
-
2.
-
Dessiner le graphe de
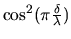 pour le rouge (
pour le rouge (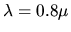 m),
le vert (
m),
le vert (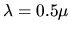 m),
l'orange (
m),
l'orange (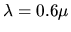 m)
et le violet (
m)
et le violet (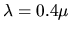 m).
On exprimera
m).
On exprimera 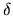 en
en 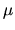 m.
Expliquer l'apparition de couleurs pour les interférences en lumière
blanche (teintes de Newton).
m.
Expliquer l'apparition de couleurs pour les interférences en lumière
blanche (teintes de Newton).
-
3.
-
Montrer qu'avec un spectre cannelé on retrouve cette échelle
des teintes pour des valeurs de
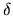 centrées en 0 et
centrées en 0 et 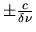 .
Les visibilités sont-elles identiques ?
.
Les visibilités sont-elles identiques ?
-
4.
-
on désire avoir 20 cannelures dans le spectre. Pour celà
on utilise comme source lumineuse la lumière recueillie en un point
du champ d'interférences de l'expérience des trous d'Young
en lumière blanche. On donne a=0.5 mm (distance des trous),
D=2 m (distance du point d'observation aux trous). Où doit
se trouver ce point ?
-
5.
-
On envoie de la lumière blanche sur une lame anisotrope à
faces parallèles (plan xy) d'épaisseur e. On
admet que la composante x du champ électrique se propage
dans la lame à la vitesse
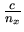 ,
la composate y se propageant à la vitesse
,
la composate y se propageant à la vitesse 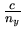 (nx et ny sont supposés indépendants
de la fréquence). La lame est placée entre un polariseur
et un analyseur placés à angle droit. Montrer que le spectre
est cannelé. Calculer le nombre de cannelures pour nx=1.454
et ny=1.459 et e=0.5 cm.
(nx et ny sont supposés indépendants
de la fréquence). La lame est placée entre un polariseur
et un analyseur placés à angle droit. Montrer que le spectre
est cannelé. Calculer le nombre de cannelures pour nx=1.454
et ny=1.459 et e=0.5 cm.
![]() ,
on désigne par
,
on désigne par ![]() le spectre de la lumière blanche. On effectue une expérience
d'interférences pour laquelle le contraste en lumière monochromatique
est 1 (trous d'Young par exemple, ou interféromètre de Michelson).
le spectre de la lumière blanche. On effectue une expérience
d'interférences pour laquelle le contraste en lumière monochromatique
est 1 (trous d'Young par exemple, ou interféromètre de Michelson).