Diffraction par un masque bidimensionnel périodique

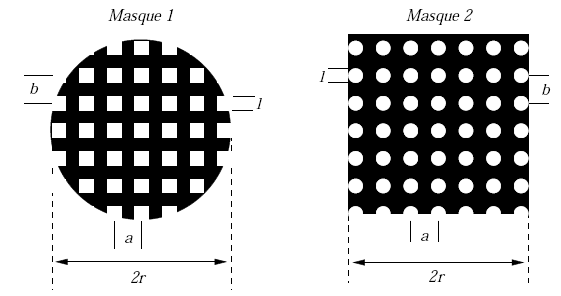
On considère les deux masques de la figure ci-après. Le premier est constitué de petits carrés opaques de côté l disposés sur les noeuds d'un maillage rectangulaire de période a dans la direction x et b dans la direction y, avec a>l et b>l. L'ensemble est limité spatialement par un diaphragme circulaire de diamètre 2r. Le deuxième masque est composé de petits disques opaques de diamètre l disposés sur les noeuds du même maillage rectangulaire, l'ensemble étant cette fois limité spatialement par un diaphragme carré de côté 2r.

L'un ou l'autre de ces masques est éclairé sous incidence normale par une onde plane monochromatique de longueur d'onde $\lambda$ et d'amplitude $\psi_0$ dans le plan du masque pris comme origine des z.

1.

Ecrire le coefficient de transmission des deux masques.

2.

Ecrire pour le masque numéro 1 l'amplitude diffractée à l'infini dans une direction $(\alpha \beta)$,$\alpha$ et $\beta$ étant les projections d'un vecteur unitaire sur les axes Ox et Oy.

3.

Mêmes questions pour le masque numéro 2.